NOIP 2008 传纸条(洛谷P1006,动态规划递推,滚动数组)

题目链接:P1006 传纸条

PS:伤心,又想不出来,看了大神的题解

AC代码:

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,m,f[][],a[][];
int main()
{
    ll i,j,k;
    cin>>n>>m;
    for (i=;i<=n;++i)
        for (j=;j<=m;++j)
            cin>>a[i][j];

    f[][]=a[][]+a[][];//不管怎样都会经过(1,2)和(2,1)先赋初值
    //i是当前的点横纵坐标之和
    //下面的循环是起码2*3或者3*2棋盘才会进入,如果2*2及以下棋盘已经初定义了
    for (i=;i<n+m;++i)//至于i<n+m我是画草图才理解的
    {
        for (j=min(i-,n);j>=;j--) //滚动数组,i层和i-层有关,所以j,k要一直减小而不是增大,防止数据覆盖
        {//j=min(i-2,n)是在不超出的情况下找尽量小的能走的位置
            for (k=min(i-,n);k>j;k--)
            {//k在j右边,所以是i-1
                if (j>)  //这里的条件判断貌似是不需要的，但加上更好
                {
                    f[j][k]=max(f[j][k],f[j-][k]);
                }
                if (j>&&k>)
                {
                    f[j][k]=max(f[j][k],f[j-][k-]);
                }
                if (k->j)//保证移动前的点没有重合
                {
                    f[j][k]=max(f[j][k],f[j][k-]);
                }
                //对于两个都从上边来的,其实是另一对(j,k)的两个都从左边来,所以不用写了
                f[j][k]+=a[j][i-j]+a[k][i-k];//把数字带上
            }
        }
    }

    cout<<f[n-][n];//输出左下角左边和上边两个格的数字和就好了

    return ;
}

点击加号展开代码

谈谈我对这个思路的理解:

1.我们可以看成两纸条同时从左上角原点出发

2.我们发现对于一个画一条条斜线,斜线上的每个点横坐标加纵坐标的和都相同

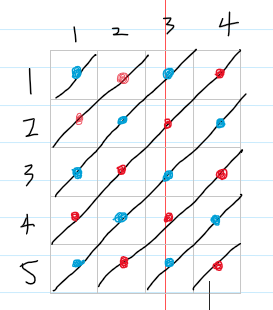
而且原点到同一条线上任意点要走的距离相同,那么每走一步,纸条a和纸条b都在一条斜线上

为了防止相遇,我们可以假设b的横坐标k永远大于a的横坐标j

而且,我们用i=n+m,那么任意一点的横坐标=i-纵坐标,纵坐标同理,也就是横坐标+纵坐标=i=n+m

3.那我们用i的变化来表示他们现在走到哪条斜线了,

这样一来,就可以开始递推,而且i只和i-1有关系,这是用滚动数组的前提

4.对于数组f[j,k],我们可以看成a走到(j,i-j),b走到(k,i-k)时捡起的总数字

5.然后赋初值,一开始第一步肯定是一个向右,一个向下,所以:

 f[][]=a[][]+a[][];

不管怎样都会经过(1,2)和(2,1)先赋初值

6.循环如何实现

for (i=;i<n+m;++i)//至于i<n+m我是画草图才理解的
    for (j=min(i-,n);j>=;j--)
//滚动数组,i层和i-层有关,所以j,k要一直减小而不是增大,防止数据覆盖
//j=min(i-2,n)是在不超出的情况下找尽量小的能走的位置
          for (k=min(i-,n);k>j;k--)//k在j右边,所以是i-1

第一维for表示要递推的次数,从4开始是因为如果n,m为1,3就没意义了,而m,n为2,2就已经靠初始化就够了,不需要递推

第二维是考虑纸条a的递推,从大到小是因为每次都要用前面的数据赋值新的数据,所以这样能防止覆盖

第三维和第二维差不多

7.递推式

if (j>)  //这里的条件判断貌似是不需要的，但加上更好
{
f[j][k]=max(f[j][k],f[j-][k]);
}
 if (j>&&k>)
{
 f[j][k]=max(f[j][k],f[j-][k-]);
}
 if (k->j)//保证移动前的点没有重合
{
 f[j][k]=max(f[j][k],f[j][k-]);
}
  //对于两个都从上边来的,其实是另一对(j,k)的两个都从左边来,所以不用写了

解释以下,这里分别代表

a从左来,b从左来

a从上来,b从左来

a从左来,b从上来

有人回问那两个都从上来去哪了?额,它其实在另外一个地方被算过了,下面上图解释

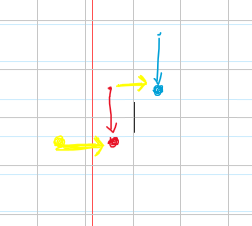
红色和蓝色表示两个都从上面来,其实他们就等于黄色的那两个地方的两个都从左边来

还有一个地方要注意的是:a从上来,b从左来,这时候要k-1>j,保证移动前的两个点不是重合的

下面上个图解释一下,下图是错误情况

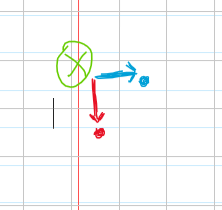
8.输出结果,只要输出当a,b到最右下角那个点的左边和上面的情况的值就好了

老是写不出来DP,自闭了...