NOI导刊2010提高（06） 黑匣子

题目描述

Black Box是一种原始的数据库。它可以储存一个整数数组，还有一个特别的变量i。最开始的时候Black Box是空的．而i等于0。这个Black Box要处理一串命令。

命令只有两种：

ADD(x):把x元素放进BlackBox;

GET:i加1，然后输出Blackhox中第i小的数。

记住：第i小的数，就是Black Box里的数的按从小到大的顺序排序后的第i个元素。例如：

我们来演示一下一个有11个命令的命令串。（如下图所示）

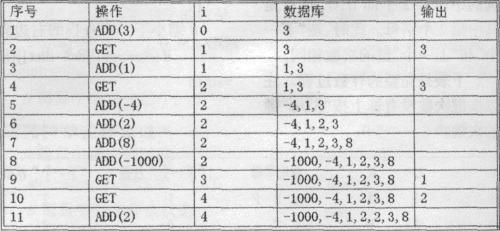
现在要求找出对于给定的命令串的最好的处理方法。ADD和GET命令分别最多200000个。现在用两个整数数组来表示命令串：

1.A(1)，A(2)，…A(M)：一串将要被放进Black Box的元素。每个数都是绝对值不超过2000000000的整数，M$200000。例如上面的例子就是A=(3，1，一4，2，8，-1000，2)。

2.u(1)，u(2)，…u(N)：表示第u(j)个元素被放进了Black Box里后就出现一个GET命令。例如上面的例子中u=(l，2，6，6)。输入数据不用判错。

输入输出格式

输入格式：

第一行，两个整数，M，N。

第二行，M个整数，表示A(l)

……A(M)。

第三行，N个整数，表示u(l)

…u(N)。

输出格式：

输出Black Box根据命令串所得出的输出串，一个数字一行。

输入输出样例

输入样例#1：
复制

7 4
3 1 -4 2 8 -1000 2
1 2 6 6

输出样例#1： 复制

3
3
1
2

说明

对于30%的数据，M≤10000;

对于50%的数据，M≤100000：

对于100%的数据，M≤200000。

思路

平衡树；

代码实现

 #include<cstdio>
 #include<algorithm>
 const int maxn=2e5+;
 int rt,ts;
 int t[maxn],sz[maxn],num[maxn];
 int f[maxn],s[maxn][];
 void rot(int x){
     int y=f[x],z=f[y],l,r;
     l=s[y][]==x?:,r=l^;
     if(y!=rt) s[z][s[z][]==y]=x;
     f[x]=z,f[y]=x,f[s[x][r]]=s[x][r]!=?y:;
     s[y][l]=s[x][r],s[x][r]=y;
     sz[y]=sz[s[y][]]+sz[s[y][]]+num[y];
     sz[x]=sz[s[x][]]+sz[s[x][]]+num[x];
 }
 void splay(int x){
     int y,z;
     while(x!=rt){
         y=f[x],z=f[y];
         if(y==rt) rot(x),rt=x;
         else{
             rot((s[z][]==y)==(s[y][]==x)?y:x),rot(x);
             if(z==rt) rt=x;
         }
     }
 }
 void ins(int k,int x){
     int fa=;
     while(k&&t[k]!=x) fa=k,++sz[k],k=s[k][x>t[k]];
     if(t[k]==x) num[k]++,sz[k]++;
     else{
         k=s[fa][x>t[fa]]=++ts;
         t[k]=x,sz[k]=,f[k]=fa,num[k]=;
     }
     splay(k);
 }
 void del(int k,int x){
     while(t[k]!=x) --sz[k],k=s[k][x>t[k]];
     num[k]--,sz[k]--;
     splay(k);
     if(!num[k]){
         rt=x=s[k][];
         while(s[x][]) sz[x]+=sz[s[k][]],x=s[x][];
         sz[x]+=sz[s[k][]],s[x][]=s[k][],f[s[k][]]=x;
     }
 }
 int search(int k,int x){
     if(x<=sz[s[k][]]) return search(s[k][],x);
     if(x<=sz[s[k][]]+num[k]) return t[k];
     return search(s[k][],x-sz[s[k][]]-num[k]);
 }
 int n,m,x,y=,ans=;
 int p[maxn];
 int main(){
     rt=++ts,t[rt]=2e9+,sz[rt]=,num[rt]=,ins(rt,-2e9-);
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;i++) scanf("%d",&p[i]);
     for(int i=;i<=m;i++){
         scanf("%d",&x);
         while(y<=x) ins(rt,p[y]),y++;
         printf("%d\n",search(rt,++ans));
     }
     return ;
 }