PCB拼板之多款矩形排样算法实现--学习
参考资料:《一种新型pcb合拼求解过程》
拼版合拼问题描述和求解过程
合拼问题描述
Pcb合拼问题是通过二维矩形组合排样而演化与扩展而形成的一种新拼版问题,把每个零件都看成一个规则的矩形进行排样 。
而PCB合拼问题中,Pcb种类多,数量大,需要多张模板拼版,母版上PCB的种类或数量不同,则母版拼版视为不同,最终优化为母版拼版种类数量。
板子的加投数与板材利用率结合,在PCB投产时一般是按照板子数量的20%进行加投。如5pcs加投2pcs ,10pcs加投2pcs,30pcs加投6pcs等等
合拼问题的求解过程
1.PCB排版算法规则
A.第一种排版规则-无序规则排版(特点:要对N种板子进行的排列组合运算,每种板子又有横竖交换排法,那就有2*A(N,N)种排法,
如有10快板子就有=2*10*9*8*7*6*5*4*3*2*1=7257600种排法,这样对于CPU的运算非常高)
合拼问题的求解过程
1.PCB排版算法规则
A.第一种排版规则-无序规则排版(特点:要对N种板子进行的排列组合运算,每种板子又有横竖交换排法,那就有2*A(N,N)种排法,
如有10快板子就有=2*10*9*8*7*6*5*4*3*2*1=7257600种排法,这样对于CPU的运算非常高)

无序排版从左到右,从上到下依次排序
B.第二种排法:Pannel折半排法(特点:板子的利用率不高)
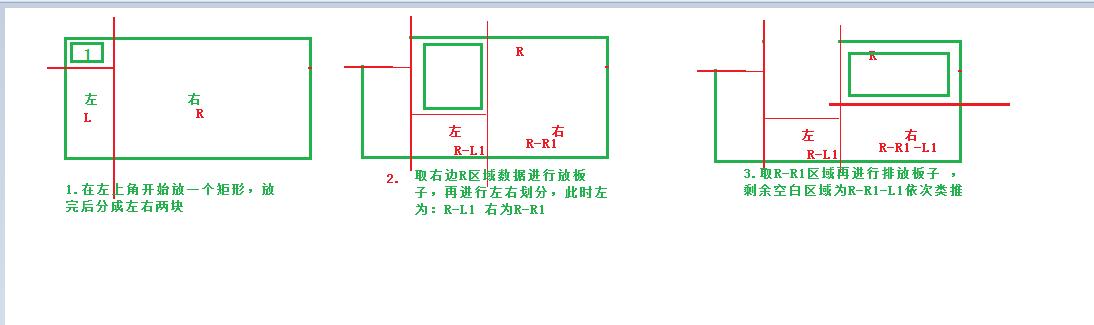
C.第三种排法:Pannel递归排法(特点:解决合拼问题,并支持扩展)
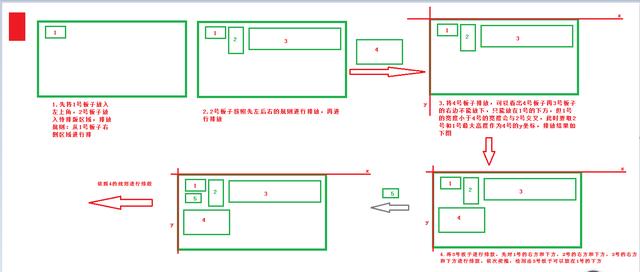
2.模拟演化过程,
当运用第三种排法的时候进行多种PCB板子进行排法 ,如图中间会产生很多空隙,该部分可如何去改造呢?

后续基于此算法研究实现
来源:参考资料:比配网 ,《一种新型pcb合拼求解过程》
排版基本参数:
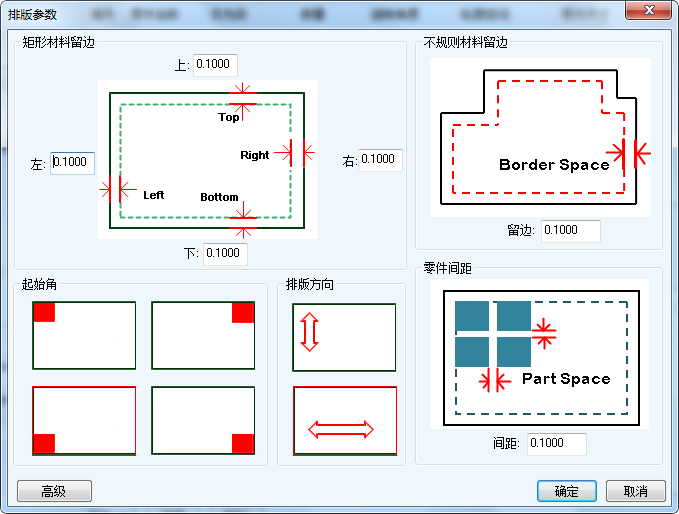
PCB拼板之多款矩形排样算法实现--学习的更多相关文章
- PCB拼板之单一矩形排样算法
算法实现相关内容整理如下: 一.排样变量与关系 此算法,基于固定4边的尺寸遍历每个单只板的长宽得到最优解. 二.条件约束 基本约束条件(参考上图变量) 三.排样图形相同类型规律 由于计算量大,为了有效 ...
- GitHub 上 57 款最流行的开源深度学习项目
转载:https://www.oschina.net/news/79500/57-most-popular-deep-learning-project-at-github GitHub 上 57 款最 ...
- Pythoner | 你像从前一样的Python学习笔记
Pythoner | 你像从前一样的Python学习笔记 Pythoner
- 【机器学习算法-python实现】採样算法的简单实现
1.背景 採样算法是机器学习中比較经常使用,也比較easy实现的(出去分层採样).经常使用的採样算法有下面几种(来自百度知道): 一.单纯随机抽样(simple random samp ...
- Tuxedo安装、配置、以及演示样例程序 (学习网址)
Tuxedo安装.配置.以及演示样例程序 (学习网址): 1.http://liu9403.iteye.com/blog/1415684 2.http://www.cnblogs.com/fnng/a ...
- 易普优APS高级计划排程系统系列提纲:行业知识,业务建模,排程算法,计划可视化,平台框架,案例分享
专注于高级计划排程系统研发与实施10来年了,国内外各种APS软件基本都研究过,这里列个提纲主要从6个方面跟大家一起讨论分享,欢迎大家鼓掌或拍砖 易普优APS高级计划排程系统系列001:行业知识,APS ...
- GitHub 上 57 款最流行的开源深度学习项目【转】
GitHub 上 57 款最流行的开源深度学习项目[转] 2017-02-19 20:09 334人阅读 评论(0) 收藏 举报 分类: deeplearning(28) from: https:// ...
- PCB拼板
- 快排 - 快速排序算法 (Chinar出品 简单易懂)
Quicksort 快排的简单讲解 本文提供全流程,中文翻译. Chinar 坚持将简单的生活方式,带给世人!(拥有更好的阅读体验 -- 高分辨率用户请根据需求调整网页缩放比例) Chinar -- ...
随机推荐
- Vue如何实现swiper左右滑动内容区控制导航tab同时切换高亮
Vue如何实现左右滑动内容区控制导航tab同时切换高亮,实现的效果是:点击导航按钮时内容区发生改变,左右滑动内容区时导航按钮跟随切换高亮,停留在某个内容区时刷新页面后仍然停留在当前内容区. ...
- Spring AOP配置简单记录(注解及xml配置方式)
在了解spring aop中的关键字(如:连接点(JoinPoint).切入点(PointCut).切面(Aspact).织入(Weaving).通知(Advice).目标(Target)等)后进行了 ...
- FPGA学习笔记(六)—— 时序逻辑电路设计
用always@(posedge clk)描述 时序逻辑电路的基础——计数器(在每个时钟的上升沿递增1) 例1.四位计数器(同步使能.异步复位) // Module Name: coun ...
- 圆角计算 Shader
圆角的计算 在Shader中,我们使用UV坐标来计算需要显示的部分和不需要显示的部分,使用透明来处理显示与不显示.UV坐标如下图1,我们将坐标平移到图2位置,面片的UV坐标原点在面片中心,UV坐标范围 ...
- selenium IDE脚本编辑与操作
1.编辑一行命令 在Table标签下选中某一行命令,命令由command.Target.value三部分组成.可以对这三部分内容那进行编辑. 然后右击这行命令,选择“Execute this comm ...
- 【ZJOI2017 Round1练习&BZOJ5354】D7T3 room(DP)
题意: 思路: 写了两种版本 考场版本 ..,..]of longint; t:..,..]of longint; n,m,i,j,k,oo,ans,d1:longint; function min( ...
- Mayor's posters POJ - 2528
The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign h ...
- 合并链表 —— 剑指Offer
题目描述 输入两个单调递增的链表,输出两个链表合成后的链表,当然我们需要合成后的链表满足单调不减规则. 思路: 也在考虑能不能更优雅的代码写法,但是最后,还是两边都写一下,能增加代码清晰度. ...
- CentOS 6.9正式版下载
2017-04-07 ,CentOS 6.9正式发布,带来了诸多改进,具体如下. CentOS 6.9重大改进: — 不再有LiveCD,用户可将LiveDVD复制到USB key,在需要时使用: ...
- TCP_NODELAY和TCP_CORK nagle算法和cork算法
TCP_NODELAY 默认情况下,发送数据採用Nagle 算法.这样尽管提高了网络吞吐量,可是实时性却减少了,在一些交互性非常强的应用程序来说是不同意的.使用TCP_NODELAY选项能够禁止Nag ...
