POJ 3621 Sightseeing Cows （最优比率环 01分数划分）

题意：

给定L个点， P条边的有向图， 每个点有一个价值， 但只在第一经过获得， 每条边有一个花费， 每次经过都要付出这个花费， 在图中找出一个环， 使得价值之和/花费之和 最大

分析：

这道题其实并不是很好想， 因为价值和花费不是在同一样东西， 价值是点， 花费是边。

但回到我们要求的问题上， 我们要找出一个最优比率的环， 那么其实每个点只会经过一次， 是一个单独的环， 所以我们可以把价值也视为边的一部分。

参考这篇博客http://blog.csdn.net/gengmingrui/article/details/47443705

用01分数划分的套路构造出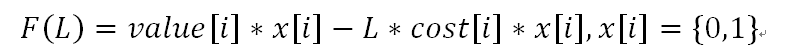

然后二分这个L， 如果这个L值跑spfa最长路存在正权环路， 说明了L太小， 存在更优的F（L）, 没有正权环路， 说明L太大， 一直二分即可有答案。

这题的坑就是没有特判， 输出3个小数位一直在找错。

SPFA

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <set>
#include <map>
#include <cstring>
#include <cmath>
#include <iomanip>
#define rep(i,a,b) for(int i = a; i < b;i++)
#define _rep(i,a,b) for(int i = a; i <= b;i++)
using namespace std;
const double eps = 1e-;
const double inf = 1e9 + ;
const int maxn =  + ;
int n , m;
double val[maxn];
struct edge{
    int to;
    double d;
    edge(int _to, double _d): to(_to), d(_d){}
};
vector<edge> G[maxn];
bool spfa(double L){ //因为答案最终一定是一个环，所以我们将每一条边的收益规定为其终点的收益，这样一个环上所有的花费和收益都能够被正确的统计。
    double dis[maxn];
    bool vis[maxn];
    int enter_cnt[maxn];//记录入队次数
    fill(dis, dis+maxn, -inf);//求最长路初始化为 负无穷
    memset(vis, , sizeof(vis));
    memset(enter_cnt, , sizeof(enter_cnt));
    queue<int> q;
    vis[] = ;
    dis[] = ;
    enter_cnt[]++;//第一次进队也要记录
    q.push();

    while(!q.empty()){
        int u = q.front();
        for(int i = ; i < G[u].size(); i++){ //求一个最长路的正权环路
            int v = G[u][i].to;
            double d = G[u][i].d;
            double w = val[v] - L * d;
            if(dis[v] < dis[u] + w){
                dis[v] = dis[u] + w;
                if(!vis[v]){
                    if(++enter_cnt[v] >= n) return true;
                    vis[v] = ;
                    q.push(v);
                }
            }
        }
        vis[u] = ;
        q.pop();
    }
    return false;
}
int main(){
//    freopen("1.txt","r", stdin);
    while(cin >> n >> m){
        _rep(i,,n) cin >> val[i];
        rep(i,,m){
            int u, v, d;
            cin >> u >> v >> d;
            G[u].push_back(edge(v,d));
        }
        double l = , r = 10000.0;
        while(abs(r - l) > eps){
            double mid = (l+r)/;
            if(spfa(mid)) //如果有环路， L太小了
            {
                l = mid;
            }
            else r = mid;
        }
        cout.setf(ios::fixed);
        cout << setprecision() << l << "\n";
        _rep(i,,n) G[i].clear();
    }
    return ;
}

Bellman

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <set>
#include <map>
#include <cstring>
#include <cmath>
#include <iomanip>
#define rep(i,a,b) for(int i = a; i < b;i++)
#define _rep(i,a,b) for(int i = a; i <= b;i++)
using namespace std;
const double eps = 1e-;
const double inf = 1e9 + ;
const int maxn =  + ;
int n , m;
double val[maxn];
struct edge{
    int to , d;
    edge(int _to, int _d): to(_to), d(_d){}
};
vector<edge> G[maxn];
bool Bellman(double L){ //因为答案最终一定是一个环，所以我们将每一条边的收益规定为其终点的收益，这样一个环上所有的花费和收益都能够被正确的统计。
    double dis[maxn];
    fill(dis, dis+maxn, -inf);

    for(int times = ; times < n - ; times++) //进行n - 1轮松弛
    {
        int flag = ;
        for(int u = ; u <= n; u++){
            for(int i = ; i < G[u].size(); i++){
                int v = G[u][i].to;
                double d = G[u][i].d;
                double w = val[v] - L * d;
                if(dis[v] < dis[u] + w){
                    flag = ;
                    dis[v] = dis[u] + w;
                }
            }
        }
        if(!flag) return false;//如果n-1次松弛前已经没有松弛， 肯定不存在正权环路
    }
     for(int u = ; u <= n; u++){
        for(int i = ; i < G[u].size(); i++){
            int v = G[u][i].to;
            double d = G[u][i].d;
            double w = val[v] - L * d;
            if(dis[v] < dis[u] + w){
                return true;
            }
        }
     }
    return false;
}
int main(){
//    freopen("1.txt","r", stdin);
    while(cin >> n >> m){
        _rep(i,,n) cin >> val[i];
        rep(i,,m){
            int u, v, d;
            cin >> u >> v >> d;
            G[u].push_back(edge(v,d));
        }
        double l = , r = 10000.0;
        while(abs(l - r) > eps){
            double mid = (l+r)/;
            if(Bellman(mid)) //如果有环路， L太小了
            {
                l = mid;
            }
            else r = mid;
        }
        cout.setf(ios::fixed);
        cout << setprecision() << l << "\n";
        _rep(i,,n) G[i].clear();
    }
    return ;
}