splay详解（一）

前言

Spaly是基于二叉查找树实现的，

什么是二叉查找树呢？就是一棵树呗:joy: ,但是这棵树满足性质—一个节点的左孩子一定比它小，右孩子一定比它大

比如说

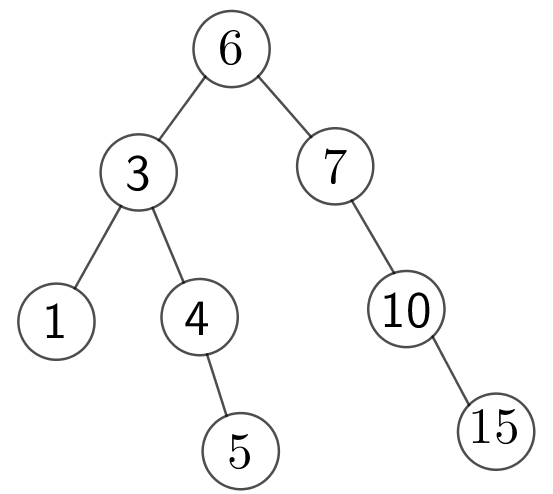
这就是一棵最基本二叉查找树

对于每次插入，它的期望复杂度大约是$logn$级别的，但是存在极端情况，比如9999999 9999998 9999997.....1这种数据，会直接被卡成$n^2$

在这种情况下，平衡树出现了！

Splay简介

Splay是平衡树的一种，中文名为伸展树，由丹尼尔·斯立特Daniel Sleator和罗伯特·恩卓·塔扬Robert Endre Tarjan在1985年发明的(mmp怎么又是tarjan)

它的主要思想是：对于查找频率较高的节点，使其处于离根节点相对较近的节点。

这样就可以保证了查找的效率

那么现在问题来了：

• 什么样的点是查找频率高的点？

这个玩意儿确实不好统计，但是你可以认为每次被查找的点查找频率相对较高，说白了就是你把每次查找到的点搬到根节点去

当然你也可以每次查找之后随机一个点作为根，于是Treaplay这种数据结构就诞生啦

•  怎么实现把节点搬到根这种操作？

这也是Splay这种数据结构所要实现的功能，接下来我们详细的介绍一下

Splay基本操作

rotate

首先考虑一下，我们要把一个点挪到根，那我们首先要知道怎么让一个点挪到它的父节点

情况1

当X是Y的左孩子

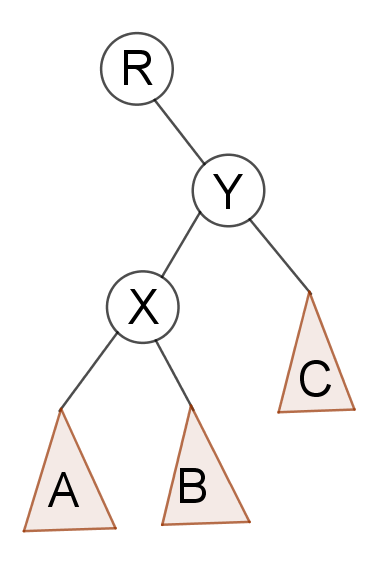
这时候如果我们让X成为Y的父亲，只会影响到3个点的关系

B与X，X与Y，X与R

根据二叉排序树的性质

B会成为Y的左儿子

Y会成为X的右儿子

X会成为R的儿子，具体是什么儿子，这个要看Y是R的啥儿子

经过变换之后，大概是这样

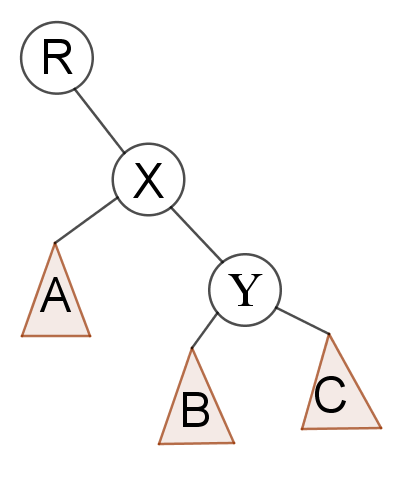
情况2

当X是Y的右孩子

本质上和上面是一样的，

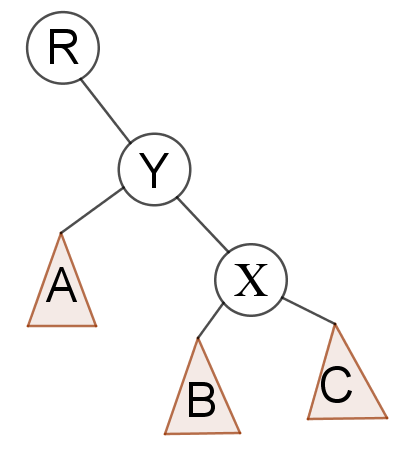
变换后为

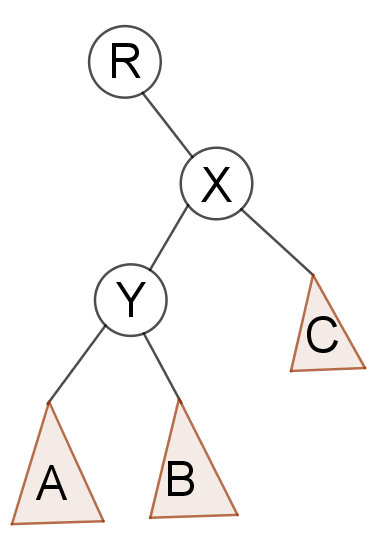
这两种代码单独实现都比较简单，我就不写了(实际上是我懒)

但是这两种旋转情况很类似，第二种情况实际就是把第一种情况的X,Y换了换位置

我们考虑一下能不能将这两种情况合并起来实现呢？

答案是肯定的

首先我们要获取到每一个节点它是它爸爸的哪个孩子，可以这么写

bool ident(int x) {
    return tree[tree[x].fa].ch[] == x ?  : ;
}

如果是左孩子的话会返回0，右孩子会返回1

那么我们不难得到R，Y，X这三个节点的信息

int Y = tree[x].fa;
int R = tree[Y].fa;
int Yson = ident(x); //x是y的哪个孩子
int Rson = ident(Y);

B的情况我们可以根据X的情况推算出来，根据^运算的性质，0^1=1,1^1=0,2^1=3,3^1=2，而且B相对于X的位置一定是与X相对于Y的位置是相反的

（否则在旋转的过程中不会对B产生影响）

int B = tree[x].ch[Yson ^ ];

然后我们考虑连接的过程

根据上面的图，不难得到

B成为Y的哪个儿子与X是Y的哪个儿子是一样的

Y成为X的哪个儿子与X是Y的哪个儿子相反

X成为R的哪个儿子与Y是R的哪个儿子相同

connect(B, Y, Yson);
connect(Y, x, Yson ^ );
connect(x, R, Rson);

connect函数这么写，挺显然的

void connect(int x, int fa, int how) { //x节点将成为fa节点的how孩子
    tree[x].fa = fa;
    tree[fa].ch[how] = x;
}

单旋函数就是这样了，利用这个函数就可以实现把一个节点搬到它的爸爸那儿了，

Splay

Splay(x,to)是实现把x节点搬到to节点

最简单的办法，对于x这个节点，每次上旋直到to

但是！

如果你真的这么写，可能会T成SB，出题人可能会构造数据把单旋卡成$n^2$，不要问我为什么！(其实是我不知道)

一个感性的理解是这样的

把一个点双旋到根，可以使得从根到它的路径上的所有点的深度变为大约原来的一半，其它点的深度最多增加2

或者你可以了解一下为啥单旋是错的

下面我们介绍一下双旋的Splay

这里的情况有很多，但是总的来说就三种情况

1.to是x的爸爸，

这样的话吧x旋转上去就好

update in 2018.2.19

这里可能写错了一个地方（其实也没有写错）

因为我们在双旋的时候会改变三个点的关系，为了方别写，所以我们开始的时候把to设置为to的爸爸

if (tree[tree[x].fa].fa == to) rotate(x);

2.x和他爸爸和他爸爸的爸爸在一条线上

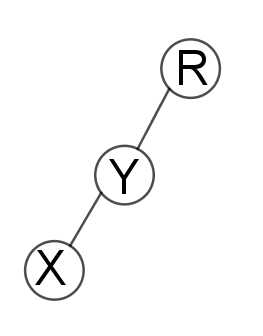
这时候先把Y旋转上去，再把X旋转上去就好

else if (ident(x) == ident(tree[x].fa)) rotate(tree[x].fa), rotate(x);

3.x和他爸爸和他爸爸的爸爸不在一条线上

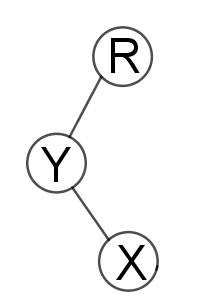
这时候把X旋转两次就好

总的代码：

void splay(int x, int to) {
    to = tree[to].fa;
    while (tree[x].fa != to) {
        if (tree[tree[x].fa].fa == to) rotate(x);
        else if (ident(x) == ident(tree[x].fa)) rotate(tree[x].fa), rotate(x);
        else rotate(x), rotate(x);
    }
}

后记

至此，Spaly的最核心最基本的操作已经讲解完毕

至于这玩意儿怎么用，以及能实现什么功能，且听下回分解