迁移学习(NRC)《Exploiting the Intrinsic Neighborhood Structure for Source-free Domain Adaptation》
论文信息
论文标题:Exploiting the Intrinsic Neighborhood Structure for Source-free Domain Adaptation
论文作者:Shiqi YangYaxing WangJoost van de WeijerLuis HerranzShangling Jui
论文来源:Neural Information Processing Systems (2021)
论文地址:download
论文代码:download
视屏讲解:click
1 介绍
域适应(DA)旨在减轻源域和目标域之间的域转移。 大多数 DA 方法需要访问源数据,但这通常是不可能的(例如,由于数据隐私或知识产权)。 在本文中,我们解决了具有挑战性的无源域自适应 (SFDA) 问题,其中源预训练模型在没有源数据的情况下适应目标域。 我们的方法基于观察到目标数据可能不再与源域分类器对齐,但仍形成清晰的集群。 我们通过定义目标数据的局部亲和力来捕获这种内在结构,并鼓励具有高局部亲和力的数据之间的标签一致性。 我们观察到更高的亲和力应该分配给互惠的邻居,并提出自正则化损失以减少嘈杂邻居的负面影响。 此外,为了聚合具有更多上下文的信息,我们考虑具有小亲和力值的扩展邻域。 在实验结果中,我们验证了目标特征的固有结构是域适应的重要信息来源。 我们证明,通过考虑局部邻居、互惠邻居和扩展邻域,可以有效地捕获这种局部结构。 最后,我们在几个 2D 图像和 3D 点云识别数据集上实现了最先进的性能。
2 背景及出发点
相关工作:
- 现有的 DA 方法在域适应训练期间依然需要源域数据,但实际上源域数据始终可以访问是不切实际的,例如当应用于具有隐私或财产限制的数据时;
问题:
- 不管开放集和封闭集的最近 DA 工作,它们都忽略了特征空间中目标数据的内在邻域结构,这对于解决 SFDA 非常有价值;
- 事实1:即使目标数据可能已经在特征空间中移动(协方差移动),但同一类的目标数据仍有望在嵌入空间中形成一个集群;Fig.1(a)
- 想法1:评估高维空间中点结构的一种行之有效的方法是考虑点的最近邻,这些点预计属于同一类;
- 事实2:Fig.1(b) 蓝色曲线表明,大约 75% 的最近邻居具有正确的标签;互惠邻居确实比非互惠最近邻居 (nRNN) 有更多机会预测真实标签;
- 想法2:使用 k 互近邻缓解最近邻部分预测错误的问题;
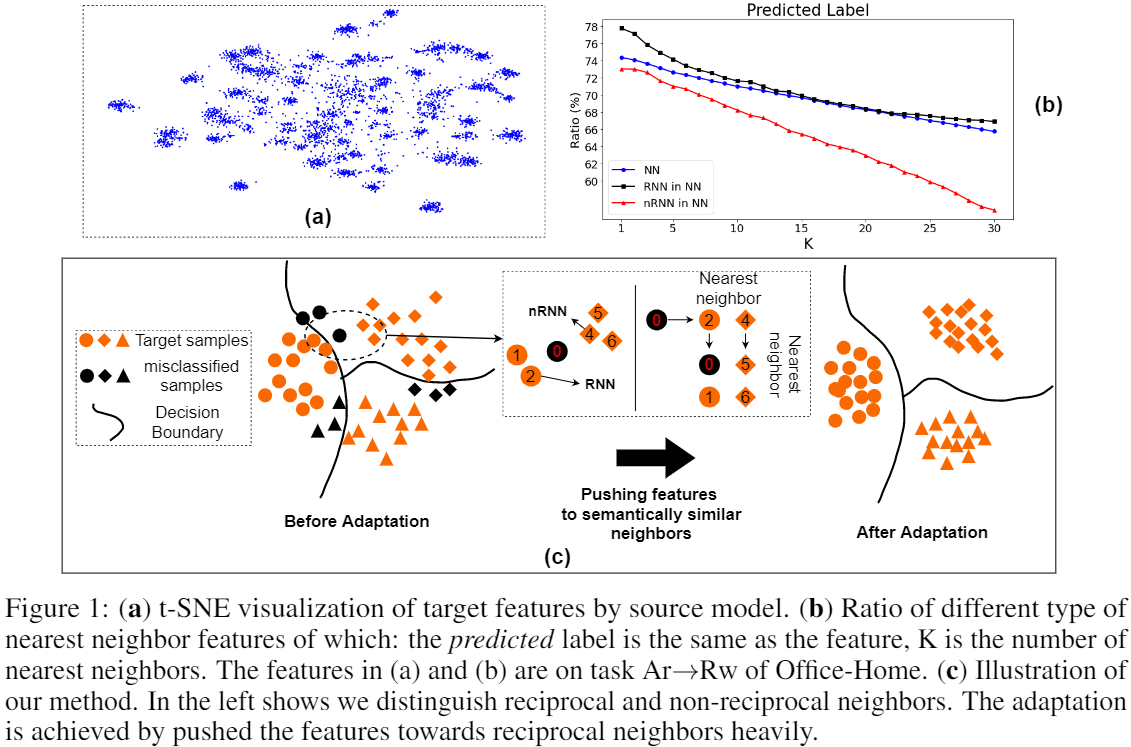
3 方法
使用源域数据训练好的源模型来生成目标域的簇结构,使用邻域信息来体现这种内在结构,并通过以下目标实现自适应:
$\mathcal{L}=-\frac{1}{n_{t}} \sum\limits _{x_{i} \in \mathcal{D}_{t}} \sum\limits_{x_{j} \in \operatorname{Neigh}\left(x_{i}\right)} \frac{D_{\text {sim }}\left(p_{i}, p_{j}\right)}{D_{d i s}\left(x_{i}, x_{j}\right)} \quad\quad\quad(1)$
其中:
- $\text{Neigh} \left(x_{i}\right)$ 为 $x_{i}$ 的最近邻集合;
- $D_{\text {sim }}$ 计算 $x_{i}$ 和其近邻之间的类分布相似性;
- $D_{d i s}$ 计算 $x_{i}$ 和其近邻之间的特征分布之间的距离;
如上述,最近邻并不一定都能带来有效监督信号,为减少这些邻居带来的潜在负面影响,本文使用连通性来权衡来自邻居的监督,即上述 $1/D_{d i s}(x_{i}, x_{j})$。
为实现 基于 batch 的最近邻训练,本文构建了两个 $\text{memory banks}$:$\mathcal{F}$ 存储所有目标特征,$\mathcal{S}$ 存储相应的预测分数:
$\mathcal{F}=\left[\boldsymbol{z}_{1}, \boldsymbol{z}_{2}, \ldots, \boldsymbol{z}_{n_{t}}\right] \text { and } \mathcal{S}=\left[p_{1}, p_{2}, \ldots, p_{n_{t}}\right]$
$\text{Note}$:简单地更新 $\text{memory bank}$ 中对应于当前 $\text{mini-batch}$ 的旧项;
对于每个样本 $x_{i}$,在 $\text{feature bank}$ 中找到它的 $k$ 个最近邻(余弦相似度),最大化它们 $\text{score}$ 的加权点积,即,使它们的输出相似或者说具有一致性。
$\mathcal{L}_{\mathcal{N}}=-\frac{1}{n_{t}} \sum\limits _{i} \sum\limits_{k \in \mathcal{N}_{K}^{i}} A_{i k} \mathcal{S}_{k}^{\top} p_{i}$
$A_{i, j}=\left\{\begin{array}{ll}1 & \text { if } j \in \mathcal{N}_{K}^{i} \wedge i \in \mathcal{N}_{M}^{j} \\r & \text { otherwise. }\end{array}\right.$
同样可以扩展到其高阶邻居:
$\mathcal{L}_{E}=-\frac{1}{n_{t}} \sum\limits_{i} \sum\limits _{k \in \mathcal{N}_{K}^{i}} \sum\limits_{m \in E_{M}^{k}} r \mathcal{S}_{m}^{\top} p_{i}$
作者没有直接使用 $\text{minimize entropy}$,而是用了一种称为 $\text{self-regularization}$ 的方法,简单来说就是最大化每个样本输出 $\text{score}$ 自己与自己的点积。不难看出当 $\text{score}$ 为 $\text{one-hot}$ 向量时点积最大,所以效果上可能和 $\text{minimize entropy}$ 差不多。
$\mathcal{L}_{\text {self }}=-\frac{1}{n_{t}} \sum\limits _{i}^{n_{t}} \mathcal{S}_{i}^{\top} p_{i}$
为了避免模型将所有数据预测为某些特定类(并且不预测任何目标数据的其他类)的退化解决方案 [8, 39],鼓励预测是平衡的。 本文采用广泛用于聚类 [8、9、13] 以及多个领域适应工作 [21、39、42] 的预测多样性损失:
$\mathcal{L}_{d i v}=\sum\limits _{c=1}^{C} \operatorname{KL}\left(\bar{p}_{c} \| q_{c}\right), \text { with } \bar{p}_{c}=\frac{1}{n_{t}} \sum\limits_{i} p_{i}^{(c)}, \text { and } q_{\{c=1, . . C\}}=\frac{1}{C}$
训练目标
$\mathcal{L}=\mathcal{L}_{\text {div }}+\mathcal{L}_{\mathcal{N}}+\mathcal{L}_{E}+\mathcal{L}_{\text {self }}$
4 实验
消融实验

A:删除亲和力 $A$ 意味着平等对待所有这些邻居;
$\mathcal{L}_{\hat{E}}$:意味着我们删除了方程式中扩展邻居的重复;
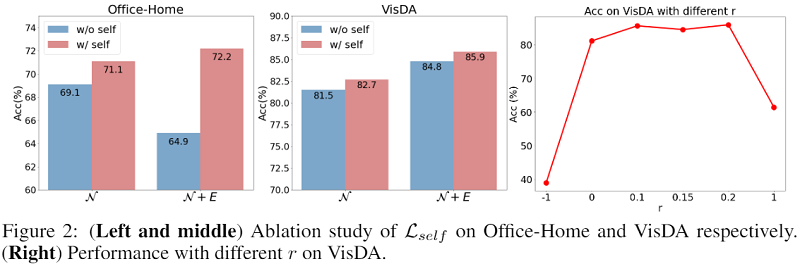
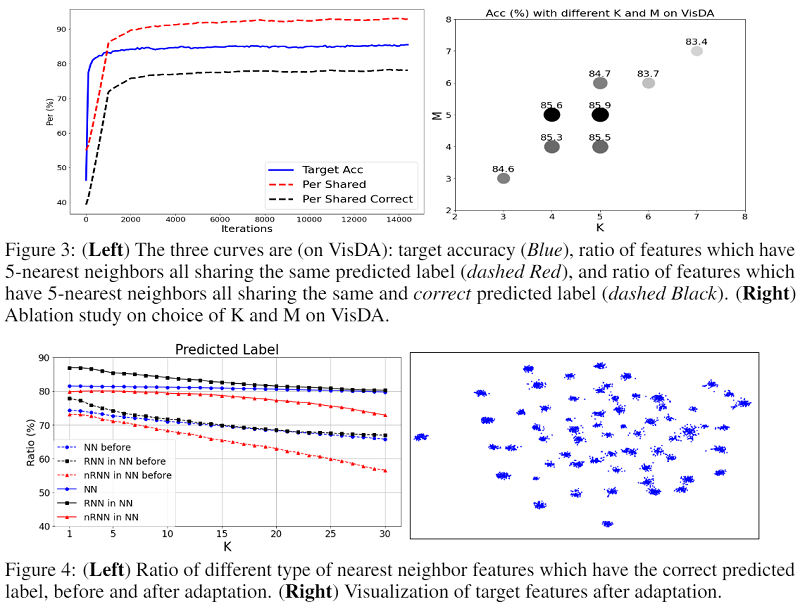
迁移学习(NRC)《Exploiting the Intrinsic Neighborhood Structure for Source-free Domain Adaptation》的更多相关文章
- 迁移学习(Transformer),面试看这些就够了!(附代码)
1. 什么是迁移学习 迁移学习(Transformer Learning)是一种机器学习方法,就是把为任务 A 开发的模型作为初始点,重新使用在为任务 B 开发模型的过程中.迁移学习是通过从已学习的相 ...
- 图像识别 | AI在医学上的应用 | 深度学习 | 迁移学习
参考:登上<Cell>封面的AI医疗影像诊断系统:机器之心专访UCSD张康教授 Identifying Medical Diagnoses and Treatable Diseases b ...
- 源码分析——迁移学习Inception V3网络重训练实现图片分类
1. 前言 近些年来,随着以卷积神经网络(CNN)为代表的深度学习在图像识别领域的突破,越来越多的图像识别算法不断涌现.在去年,我们初步成功尝试了图像识别在测试领域的应用:将网站样式错乱问题.无线领域 ...
- 迁移学习( Transfer Learning )
在传统的机器学习的框架下,学习的任务就是在给定充分训练数据的基础上来学习一个分类模型:然后利用这个学习到的模型来对测试文档进行分类与预测.然而,我们看到机器学习算法在当前的Web挖掘研究中存在着一个关 ...
- 【迁移学习】2010-A Survey on Transfer Learning
资源:http://www.cse.ust.hk/TL/ 简介: 一个例子: 关于照片的情感分析. 源:比如你之前已经搜集了大量N种类型物品的图片进行了大量的人工标记(label),耗费了巨大的人力物 ...
- 迁移学习(Transfer Learning)(转载)
原文地址:http://blog.csdn.net/miscclp/article/details/6339456 在传统的机器学习的框架下,学习的任务就是在给定充分训练数据的基础上来学习一个分类模型 ...
- 迁移学习-Transfer Learning
迁移学习两种类型: ConvNet as fixed feature extractor:利用在大数据集(如ImageNet)上预训练过的ConvNet(如AlexNet,VGGNet),移除最后几层 ...
- [DeeplearningAI笔记]ML strategy_2_3迁移学习/多任务学习
机器学习策略-多任务学习 Learninig from multiple tasks 觉得有用的话,欢迎一起讨论相互学习~Follow Me 2.7 迁移学习 Transfer Learninig 神 ...
- Gluon炼丹(Kaggle 120种狗分类,迁移学习加双模型融合)
这是在kaggle上的一个练习比赛,使用的是ImageNet数据集的子集. 注意,mxnet版本要高于0.12.1b2017112. 下载数据集. train.zip test.zip labels ...
- 【深度学习系列】迁移学习Transfer Learning
在前面的文章中,我们通常是拿到一个任务,譬如图像分类.识别等,搜集好数据后就开始直接用模型进行训练,但是现实情况中,由于设备的局限性.时间的紧迫性等导致我们无法从头开始训练,迭代一两百万次来收敛模型, ...
随机推荐
- Notepad++中文设置
找到问题所在了,作者改了个小代码,在安装目录下打开localization找到chineseSimplified,打开后,在852行那里找到下面这段代码 <MarginsBorderEdge t ...
- 【python】第一模块 步骤四 第一课、初始正则表达式
第一课.初始正则表达式 一.课程介绍 1.1 课程概要 步骤介绍 正则表达式入门及应用 正则的进阶 案例 综合项目实战 二.正则表达式的基本操作(多敲代码多做练习) 2.1 什么是正则表达式 什么是正 ...
- STL二分查找算法
二分法检索又称折半检索,二分法检索的基本思想是设字典中的元素从小到大有序地存放在数组(array)中,首先将给定值key与字典中间位置上元素的关键码(key)比较,如果相等,则检索成功:否则,若key ...
- 【Unity】Lua热重载
写在前面 本文讨论的"Lua热重载"是基于他人现成工具和相关博文上展开的,所以这里并不会重复实现一遍工具,主要记录我的理解过程. Lua热重载 探索 偶然在知乎上翻到一篇文章&qu ...
- test.sh 监听进程是否存在
监听myloader进程是否结束,结束后把时间输出到 /root/time.log vim test.sh #!/bin/bash #确保PRO查询进程唯一 PRO="myloader&qu ...
- centos7部署teleport堡垒机
Centos7.9部署Teleport堡垒机 简介 Teleport是一款简单易用的开源堡垒机系统,具有小巧.易用的特点,支持 RDP/SSH/SFTP/Telnet 协议的远程连接和审计管理.Tel ...
- Audition导入视频文件出现错误
错误: We were unable to open this file using any of the currently available importers. If you would li ...
- CentOS7 安裝DHCP服務並啟用DHCP failover
1. 安裝dhcp服務 yum install -y dhcp 2. host1 vi /etc/dhcp/dhcpd.failover failover peer "dhcpfailove ...
- 在DeepIn系统中使用eclipse创建maven的Web项目
1. 安装好jdk和eclipse以后,启动eclipse 2. 创建maven项目,选择Maven Project 3. 在创建项目过程中,创建简单Maven项目,不使用archetype创建(会联 ...
- C# .netCore 上传文件到ftps/ftp
白码一号的博客园 最近由于项目安全需要,将之前的ftp上传文件的方式,改用ftps 因为不太了解这个东西便开始了踩坑之旅 首先,最近在ubuntu 上搭建了这个服务 流程可以参考这些博客(部署网上的资 ...
