Mathematica做数字图像处理中的ImageConvolve练习

目录

• ImageConvolve练习
  • • original
    • right sobel 垂直边检测
    • top sobel 水平边检测
    • 通过一个平方内核的卷积使图像变平滑
    • 类似ConstantArray[1, {1, 21}]/21.这样的水平行向量来做水平方向模糊
    • 做竖直方向模糊
    • emboss，浮雕效果
    • 高斯模糊
    • sharpen锐化
    • outline(also called "edge" kernel)

基本的操作做起来很方便，

更高级的话还是建议open cv或者photoshop这样的

图像卷积的原理：找到一篇文章讲得很清楚

ImageConvolve练习

给出image和kernel的卷积



padding是说对image外围进行填充，用全0，还是Extrapolation，或者其他的

不然卷积得到的图像的size比image小

original

Import@"ExampleData/applepicking.jpg"

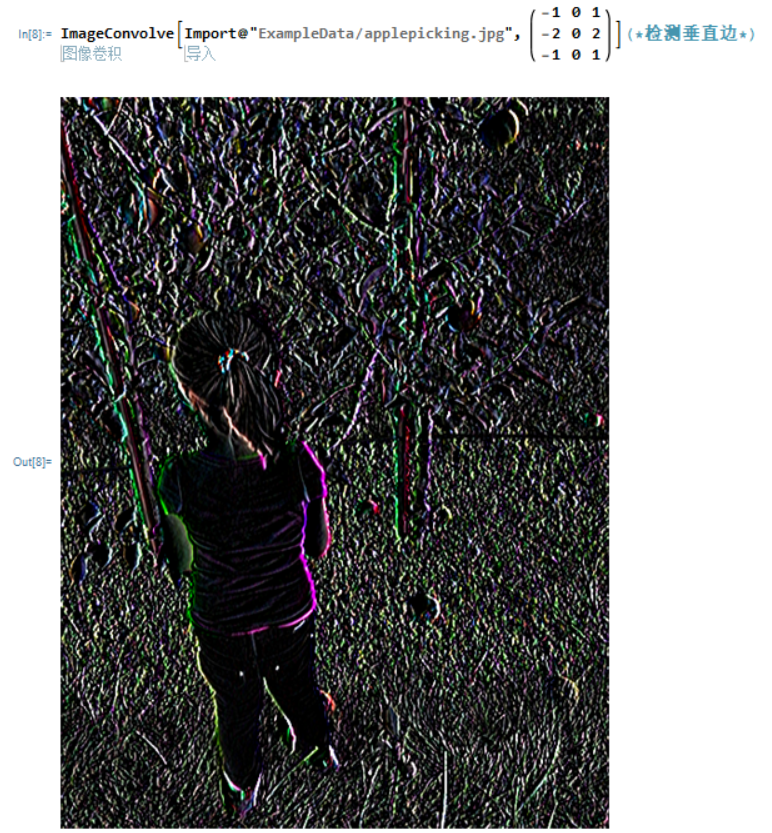
right sobel 垂直边检测

下面的是输入文本形式，复制粘贴过去shift enter就能运行了

ImageConvolve[Import@"ExampleData/applepicking.jpg", \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{
RowBox[{"-", "1"}], "0", "1"},
{
RowBox[{"-", "2"}], "0", "2"},
{
RowBox[{"-", "1"}], "0", "1"}
},
GridBoxAlignment->{
       "Columns" -> {{Center}}, "ColumnsIndexed" -> {},
        "Rows" -> {{Baseline}}, "RowsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}, "RowsIndexed" -> {}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)](*检测垂直边*)

之所以说right sobel 是看1，2，1确实是在正右方

top sobel 水平边检测

ImageConvolve[Import@"ExampleData/applepicking.jpg", \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"1", "2", "1"},
{"0", "0", "0"},
{
RowBox[{"-", "1"}],
RowBox[{"-", "2"}],
RowBox[{"-", "1"}]}
},
GridBoxAlignment->{
       "Columns" -> {{Center}}, "ColumnsIndexed" -> {},
        "Rows" -> {{Baseline}}, "RowsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}, "RowsIndexed" -> {}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)](*检测水平边*)

之所以说top sobel 是看1，2，1确实是在正上方

通过一个平方内核的卷积使图像变平滑

ImageConvolve[Import@"ExampleData/applepicking.jpg",
 BoxMatrix[1]/9](*{{1/9,1/9,1/9},{1/9,1/9,1/9},{1/9,1/9,1/9}},使图像平滑*)

类似ConstantArray[1, {1, 21}]/21.这样的水平行向量来做水平方向模糊

ImageConvolve[Import@"ExampleData/applepicking.jpg",
 ConstantArray[1, {1, 21}]/21.](*水平方向模糊*)

做竖直方向模糊

ImageConvolve[Import@"ExampleData/applepicking.jpg",
 ConstantArray[1, {21, 1}]/21.](*竖直方向模糊*)

emboss，浮雕效果

ImageConvolve[Import@"ExampleData/applepicking.jpg", \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{
RowBox[{"-", "2"}],
RowBox[{"-", "1"}], "0"},
{
RowBox[{"-", "1"}], "1", "1"},
{"0", "1", "2"}
},
GridBoxAlignment->{
       "Columns" -> {{Center}}, "ColumnsIndexed" -> {},
        "Rows" -> {{Baseline}}, "RowsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}, "RowsIndexed" -> {}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)](*emboss实现浮雕效果*)

高斯模糊

ImageConvolve[Import@"ExampleData/applepicking.jpg",
 GaussianMatrix[30]](*高斯模糊，或者叫毛玻璃？*)

我不是很懂这个，我猜毛玻璃效果就是拿高斯模糊做的？

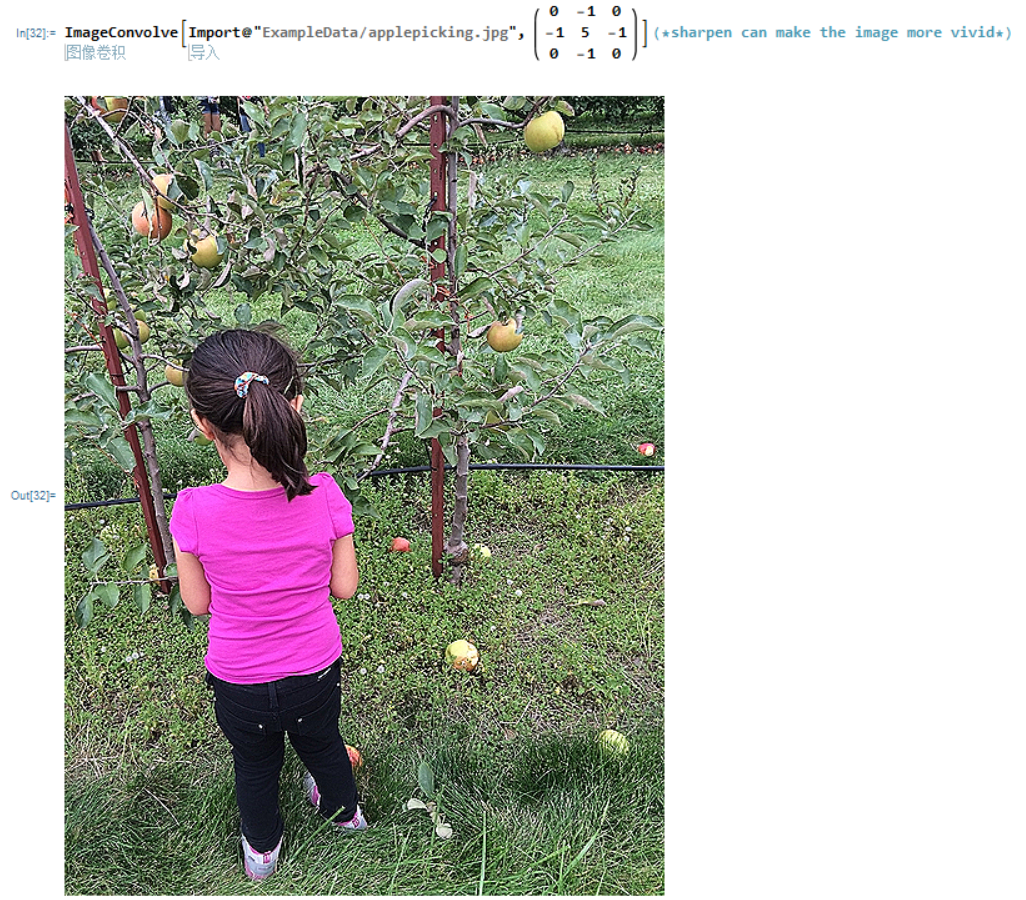
sharpen锐化

ImageConvolve[Import@"ExampleData/applepicking.jpg", \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"0",
RowBox[{"-", "1"}], "0"},
{
RowBox[{"-", "1"}], "5",
RowBox[{"-", "1"}]},
{"0",
RowBox[{"-", "1"}], "0"}
},
GridBoxAlignment->{
       "Columns" -> {{Center}}, "ColumnsIndexed" -> {},
        "Rows" -> {{Baseline}}, "RowsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}, "RowsIndexed" -> {}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)](*sharpen can make the image more vivid*)

The sharpen kernel emphasizes differences in adjacent pixel values. This makes the image look more vivid.

outline(also called "edge" kernel)

ImageConvolve[Import@"https://img2020.cnblogs.com/blog/1943228/202102/1943228-20210211120157952-1609166322.png", \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{
RowBox[{"-", "1"}],
RowBox[{"-", "1"}],
RowBox[{"-", "1"}]},
{
RowBox[{"-", "1"}], "8",
RowBox[{"-", "1"}]},
{
RowBox[{"-", "1"}],
RowBox[{"-", "1"}],
RowBox[{"-", "1"}]}
},
GridBoxAlignment->{
       "Columns" -> {{Center}}, "ColumnsIndexed" -> {},
        "Rows" -> {{Baseline}}, "RowsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}, "RowsIndexed" -> {}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)](*outline*)

结果如下图所示，可以看到效果一般，

可以使用很多更加有效的方法

反正万物皆可AI,DL,RL,NN。。。。。。