二叉树：前序遍历、中序遍历、后序遍历，BFS，DFS

1.定义

一棵二叉树由根结点、左子树和右子树三部分组成，若规定 D、L、R 分别代表遍历根结点、遍历左子树、遍历右子树，则二叉树的遍历方式有 6 种：DLR、DRL、LDR、LRD、RDL、RLD。由于先遍历左子树和先遍历右子树在算法设计上没有本质区别，所以，只讨论三种方式：

DLR根左右--前序遍历（根在前，从左往右，一棵树的根永远在左子树前面，左子树又永远在右子树前面 ）

LDR左根右--中序遍历（根在中，从左往右，一棵树的左子树永远在根前面，根永远在右子树前面）

LRD左右根--后序遍历（根在后，从左往右，一棵树的左子树永远在右子树前面，右子树永远在根前面）

例如：

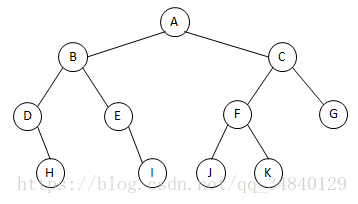
先(根)序遍历（根左右）：A B D H E I C F J K G

中(根)序遍历（左根右） : D H B E I A J F K C G

后(根)序遍历（左右根） : H D I E B J K F G C A

2.程序实现

Python实现

#节点类
class node():
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

# 先序遍历
def preOrder(n):
    if n == None:
        return
    print(n.value,  end=" ")
    preOrder(n.left)
    preOrder(n.right)

# 中序遍历
def middleOrder(n):
    if n == None:
        return
    middleOrder(n.left)
    print(n.value, end=" ")
    middleOrder(n.right)

# 后序遍历
def postOrder(n):
    if n == None:
        return
    postOrder(n.left)
    postOrder(n.right)
    print(n.value, end=" ")

if __name__ == '__main__':
    a,b,c,d,e,f = node('a'),node('b'),node('c'),node('d'),node('e'),node('f')
    a.left = b
    a.right = e
    b.left = c
    b.right = d
    e.right = f
    preOrder(a)
    print()
    middleOrder(a)
    print()
    postOrder(a)

　　　　a

　　　 /      \

　　b　　　　e

/      \　　　　\

c           d　　　    f

输出

a b c d e f
c b d a e f
c d b f e a

C实现

typedef struct TreeNode
{
    int data;
    TreeNode * left;
    TreeNode * right;
    TreeNode * parent;
}TreeNode;

void pre_order(TreeNode * Node)//前序遍历递归算法
{
    if(Node == NULL)
        return;
    printf("%d ", Node->data);//显示节点数据，可以更改为其他操作。在前面
    pre_order(Node->left);
    pre_order(Node->right);
}
void middle_order(TreeNode *Node)//中序遍历递归算法
{
    if(Node == NULL)
        return;
    middle_order(Node->left);
    printf("%d ", Node->data);//在中间
    middle_order(Node->right);
}
void post_order(TreeNode *Node)//后序遍历递归算法
{
    if(Node == NULL)
        return;
    post_order(Node->left);
    post_order(Node->right);
    printf("%d ", Node->data);//在最后
}

3.求二叉树结构

例题1：

已知某二叉树的前序遍历为A-B-D-F-G-H-I-E-C,中序遍历为F-D-H-G-I-B-E-A-C,请还原这颗二叉树。

解题思路：

从前序遍历中，我们确定了根结点为A，在从中序遍历中得出 F-D-H-G-I-B-E在根结点的左边，C在根结点的右边，那么我们就可以构建我们的二叉树的雏形。

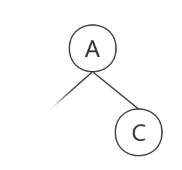
那么剩下的前序遍历为B-D-F-G-H-I-E，中序遍历为F-D-H-G-I-B-E， B就是我们新的“根结点”，从中序遍历中得出F-D-H-G-I在B的左边，E在B的右边，继续构建

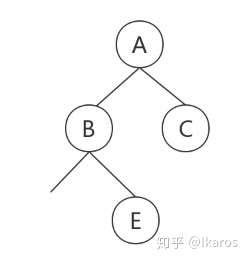
那么剩下的前序遍历为D-F-G-H-I，中序遍历为F-D-H-G-I，D就是我们新的“根结点”，从中序遍历中得出F在D的左边，H-G-I在D的右边，继续构建

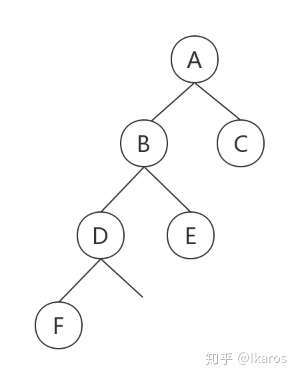
那么剩下的前序遍历为G-H-I，中序遍历为H-G-I，G就是我们新的“根结点”，从中序遍历中得出H在G的左边，I在G的右边，继续构建

例题2：

已知某二叉树的中序遍历为F-D-H-G-I-B-E-A-C,后序遍历为F-H-I-G-D-E-B-C-A,请还原这颗二叉树。

解题思路：

从后序遍历中，我们确定了根结点为A，在从中序遍历中得出 F-D-H-G-I-B-E 在根结点的左边，C在根结点的右边，那么我们就可以构建我们的二叉树的雏形。之后就是新根节点B，FDHGI在根左，E在根右。在之后就是新根D，F根左，HGI根右，然后就差不多了。

和前序和中序还原二叉树一样，我们同理可以通过中序和后序还原二叉树。

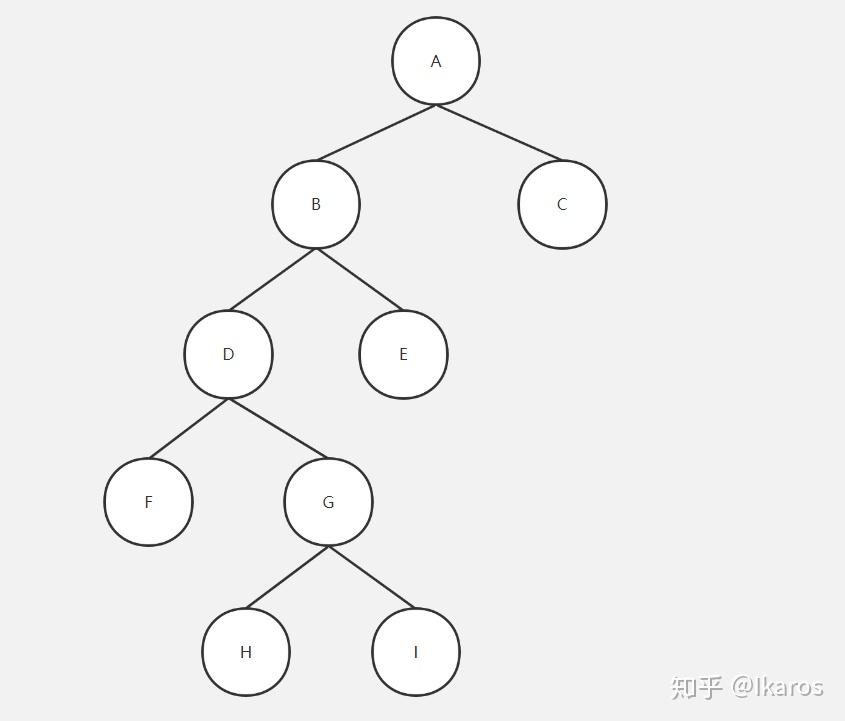
光有前序遍历和后序遍历是无法还原二叉树的。

4.BFS和DFS

BFS（广度优先遍历，Breadth First Search）及DFS（深度优先遍历，Depth First Search）是遍历树或图的两种最常用的方法。

参考

https://blog.csdn.net/u013834525/article/details/80421684

https://blog.csdn.net/qq_34840129/article/details/80619761

https://zhuanlan.zhihu.com/p/73438175

https://blog.csdn.net/Gene1994/article/details/85097507