LCS&&LRC&&LIS问题

　　注：最近笔试题经常碰到DP动态规划的问题，但是由于本人没有接触过DP，笔试后看到别人家的答案简洁又漂亮，真的羡慕；难的DP自己可能不会，那再见到常见的LCS和LRS以及LIS为问题总该会吧；

　　资料参考：segmentfault：：SecondLife：：https://segmentfault.com/a/1190000002641054 （作者的时间复杂度为nlogn的LIS实现有些问题，在这进行改正）

一：LCS（非连续最长公共子序列）

   　问题：输入两个字符串 BDCABA 和 ABCBDAB，字符串 BCBA 和 BDAB 都是是它们的最长公共子序列，则输出它们的长度 4，并打印任意一个子序列. （Note: 不要求连续）

　　DP分析：时间复杂度 O(m*n)

1. 假设两个字符串为：X=[x1,x2,....,xm]和Y=[y1,y2,...,yn]，最长LSC=[z1,z2,...,zk]；
   
2. 假设当前比较位置是xm与yn：
   • if xm==yn , 那么 Zk-1 是 Xm-1 和 Yn-1 的最长公共子序列；
   • else          ，那么z是 （Xm-1和Yn）或者（Xm和Yn-1）够成的较长的一个LCS；
3. 使用二维数组c[i][j]保存Xi与Yj时构成的LCS长度：

　　　　

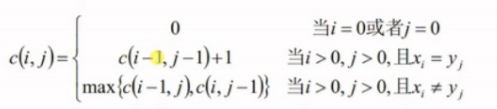
Java实现：

public class LCS最长公共子序列 {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        char []s1=sc.nextLine().trim().toCharArray();
        char []s2=sc.nextLine().trim().toCharArray();
        sc.close();
        int[][]c=new int[s1.length+1][s2.length+1];
        for(int i=1;i<=s1.length;i++){
            for(int j=1;j<=s2.length;j++){
                if(s1[i-1]==s2[j-1]){
                    c[i][j]=c[i-1][j-1]+1;
                }else{
                    c[i][j]=Math.max(c[i-1][j],c[i][j-1]);
                }
            }
        }
        System.out.println("生成的动态规划表为：");
        for(int[]tem:c){
            System.out.println(Arrays.toString(tem));
        }
        StringBuilder sb=new StringBuilder();
       print(sb,s1,s2,c,c.length-1,c[0].length-1);
        System.out.println("其中一个子串序列为："+sb.reverse().toString());
    }

    private static void print(StringBuilder sb, char[] s1, char[] s2, int[][] c, int i, int j){
        if(i==0||j==0)
            return;
        else if (s1[i-1]==s2[j-1]){
            sb.append(s1[i-1]);
            print(sb,s1,s2,c,i-1,j-1);
        }else if(c[i-1][j]>c[i][j-1]){
            print(sb,s1,s2,c,i-1,j);
        }else{
            print(sb,s1,s2,c,i,j-1);
        }
    }
}

二：LRC（最长连续公共子串）

　　问题：定义 2 个字符串 query 和 text, 如果 query 里最大连续字符子串在 text 中存在，则返回子串长度. 例如: query="acbac"，text="acaccbabb"， 则最大连续子串为 "cba", 则返回长度 3.　

　   DP分析：时间复杂度 O(m*n)

• • 我们使用c[i,j] 表示 以 Xi 和 Yj 结尾的最长公共子串的长度，因为要求子串连续，所以对于 Xi 与 Yj来讲，它们要么与之前的公共子串构成新的公共子串；要么就是不构成公共子串。故状态转移方程

　　状态转移方程为：

X[i-1] == Y[j-1]，c[i,j] = c[i-1,j-1] + 1；

X[i-1] != Y[j-1]，c[i,j] = 0；

　　Java实现：

public class LRC最长公共子串 {

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        char []s1=sc.nextLine().trim().toCharArray();
        char []s2=sc.nextLine().trim().toCharArray();
        sc.close();
        int[][]c=new int[s1.length+1][s2.length+1];
        int maxlen=0;
        for(int i=1;i<=s1.length;i++){
            for(int j=1;j<=s2.length;j++){
                if(s1[i-1]==s2[j-1]){
                    c[i][j]=c[i-1][j-1]+1;  //从c[i][j]位置保存了当前最长子串长度信息；
                    maxlen=Math.max(maxlen,c[i][j]);
                }
            }
        }
        System.out.println("生成的动态规划表为：");
        for(int[]tem:c){
            System.out.println(Arrays.toString(tem));
        }
        System.out.println("最长子串为："+maxlen);
    }
}

三：LIS（非连续最长递增公共子序列）O(n^2)实现

　　问题：问题描述：找出一个n个数的序列的最长单调递增子序列： 比如A = {5,6,7,1,2,8} 的LIS是5,6,7,8

　　DP分析：时间复杂度 O(n^2)

dp[i]表示以i位置结尾的递增序列的最大长度；
dp[i]= |---  0  if i=0;
       |---  Max(dp[j])+1  if s[i]>s[j] forall j<i;
       |---  否则不必更新dp[i]；dp[j]表示已j位置结尾的递增序列的最大长度；

Java实现：

public class LIS最长递增子序列 {
    public static void main(String[] args) {

        Scanner sc = new Scanner(System.in);
        String[]tem=sc.nextLine().trim().split(" ");
        int[]s=new int[tem.length];
        for (int i=0;i<s.length;i++){
            s[i]=Integer.valueOf(tem[i]);
        }
        int maxlen=0;
        int bestEnd=0;//保存最长递增子序列的结尾；
        int[] dp=new int[s.length];//DP数组；
        int[] pre=new int[s.length];//保存最长递增子序列的编号；
        dp[0]=1;
        pre[0]=-1;
        for(int i=1;i<dp.length;i++){
            for(int j=0;j<i;j++){
                if(dp[j]+1>dp[i]&&s[i]>s[j]){
                    dp[i]=dp[j]+1;
                    pre[i]=j;//i 的前一位是 j；
                }
            }
           if(dp[i]>maxlen){
                maxlen=dp[i];
                bestEnd=i;
           }
        }
        System.out.println("动态规划数组为："+ Arrays.toString(dp));
        StringBuilder sb=new StringBuilder();
        while(bestEnd>=0){
            sb.append(s[bestEnd]);
            bestEnd=pre[bestEnd];
        }
        System.out.println("最长的递增子序列为：");
        System.out.println(sb.reverse().toString());
    }
}

四：LIS（非连续最长递增公共子序列） O(nlogn)实现

　　DP分析：O(nlogn)

• 1. arr[i] > MaxV[nMaxLength], 将arr[i]插入到MaxV[++nMaxLength]的末尾 -- 意味着我们找到了一个新的最大LIS
  
• 2. arr[i] <= MaxV[nMaxLength], 找到MaxV[]中刚刚大于arr[i]的元素，arr[j].arr[i]替换arr[j]
  因为MaxV是一个有序数组，查找过程可以使用log(N)的折半查找。
  这样运行时间: n个整数和每个都需要折半查找 -- n*logn = O(nlogn)　　

Java实现：

public class LIS最长递增子序列nlogn的解法 {
    public static void main(String[] args) {
        Scanner scanner=new Scanner(System.in);
        //输入自定义数组arr的大小；
        int n= scanner.nextInt();
//      int []arr={11, 21, 6, 4, 29, 4, 20, 22, 8, 6};
        int[]arr=new int[n];Random random=new Random();
        //生成arr数组；
        for(int i=0;i<arr.length;i++){arr[i]=random.nextInt(31);}
        System.out.println("arr："+Arrays.toString(arr));

        int []maxV=new int[arr.length];//保存递增子序列；
        int []LIS=new int[arr.length]; // LIS[i]表示以arr[i]结尾的最长递增子序列的长度；
        maxV[0]=arr[0];
        LIS[0]=1;
        int len=0;
        int maxLen=1;
        for(int i=1;i<arr.length;i++){
            if(arr[i]>maxV[len]){
                maxV[++len]=arr[i];
                LIS[i]=len+1;
                maxLen=Math.max(maxLen,len+1);
            }else{
                int index=binChange(maxV,arr[i],0,len);
                maxV[index]=arr[i];
                LIS[i]=index+1;
            }
        }
        System.out.println("LIS:"+Arrays.toString(LIS));
        System.out.println("最长LIS为："+maxLen);
        //以下为：输出其中的一个递增子字符串：
        Stack<Integer>stack=new Stack<>();
        for(int i=LIS.length-1;i>=0&&maxLen>0;i--){
            if(LIS[i]==maxLen){
               stack.push(arr[i]);
                maxLen--;
            }
        }
       while (!stack.isEmpty()){
           System.out.print(stack.pop()+" ");
       }
    }
    private static int binChange(int[] maxV, int tem, int str, int end) {
        while(str<end){
            int mid=str+(end-str)/2;
            if(maxV[mid]==tem){
                return mid;
            }else if(maxV[mid]>tem){
                end=mid;//mid有可能是待寻找的位置；
            }else{
                str=mid+1;
            }
        }
        return str;
    }
}