Cow Picnic S 更新了（在后面）

解题思路： 从每头奶牛的节点开始做搜索，用dfs走遍所有路径（走到底，不回头）。每遍历到一个节点该节点遍历次数就加一，最后所有奶牛都搜索完之后，检查每个节点的遍历次数，如果该节点的遍历次数等于奶牛数则该节点能被所有奶牛走到。

坑：

1.每头奶牛搜索的时候要有清空的vis数组记录走没走过该点，否则可能路径会重复循环。

2.要用邻接矩阵mp[i][j]来记录节点的连接关系 ，其中i 是起点的编号 ， j  是终点的编号， 矩阵的值为1时表示i 到 j 可以连接，0表示没有。

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int N=1010;
 4 int k,n,m,l[N]={0},vis[N]={0},mp[N][N]={0},vis1[N]={0};
 5 void dfs(int x)
 6 {
 7     vis1[x]=1;
 8     vis[x]++;
 9     for(int i=1;i<=n;i++)
10     {
11         if(mp[x][i]==1&&vis1[i]==0)
12         {
13             dfs(i);
14         }
15     }
16 }
17 int main()
18 {
19     cin>>k>>n>>m;
20     for(int i=1;i<=k;i++)
21     {
22         scanf("%d",&l[i]);
23     }
24     for(int i=1;i<=m;i++)
25     {
26         int a1,b;
27         scanf("%d%d",&a1,&b);
28         mp[a1][b]=1;
29     }
30     for(int i=1;i<=k;i++)
31     {
32         memset(vis1,0,sizeof(vis1));
33         dfs(l[i]);
34     }
35     int ans=0;
36     for(int i=1;i<=n;i++)
37     {
38         if(vis[i]==k) ans++;
39     }
40     cout<<ans<<endl;
41     return 0;
42 }

更新了：

有优化方案：

新思路≈图存储方式、遍历方式优化

就用一个vector（二维）来记录一个节点跟所有连接节点的关系。

还有亿个细节值得注意：

因为这里是有向表所以 1 edge[a1].push_back(b);

如果是无向表 1 edge[a1].push_back(b); 2 edge[b].push_back(a1);

以及dfs中的for循环要改一下。i的范围：  [0,edge[x].size()-1]

效果：

存储效率，循环效率更高

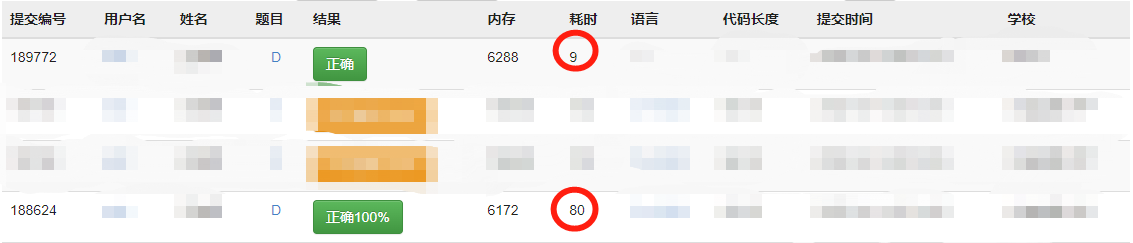
效果如图所示，提交编号为188624的为优化前的提交记录耗时80ms，提交编号为189772的为优化后的提交记录耗时9ms

程序：

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int N=1005;
 4 int k,n,m,l[N]={0},vis[N]={0},mp[N][N]={0},vis1[N]={0};
 5 vector<int> edge[N];
 6 void dfs(int x)
 7 {
 8     vis1[x]=1;
 9     vis[x]++;
10     for(int i=0;i<edge[x].size();i++)
11     {
12         if(vis1[edge[x][i]]==0)
13         {
14             dfs(edge[x][i]);
15         }
16     }
17 }
18 int main()
19 {
20     cin>>k>>n>>m;
21     for(int i=1;i<=k;i++)
22     {
23         scanf("%d",&l[i]);
24     }
25     for(int i=1;i<=m;i++)
26     {
27         int a1,b;
28         scanf("%d%d",&a1,&b);
29         edge[a1].push_back(b);
30     }
31     for(int i=1;i<=k;i++)
32     {
33         memset(vis1,0,sizeof(vis1));
34         dfs(l[i]);
35     }
36     int ans=0;
37     for(int i=1;i<=n;i++)
38     {
39         if(vis[i]==k) ans++;
40     }
41     cout<<ans<<endl;
42     return 0;
43 }