P1350 车的放置 题解

一、题目描述：

　　给你一个网格棋盘，a,b,c,d 表示了对应边长度，也就是对应格子数。

　　例如，当 a=b=c=d=2 时，对应了下面这样一个棋盘：

　　　　　　　　　　

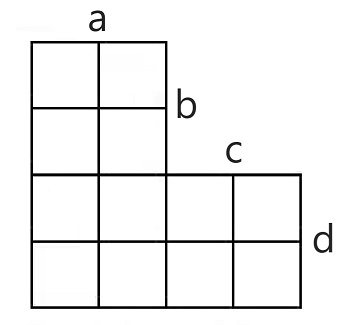
　　想要在这个棋盘上放 k 棋子，也就是这 k 个棋子没有两个在同一行，也没有两个在同一列，问有多少种方案。

　　答案对 1e5+3 取模。数据保证 0 <= a,b,c,d,k <= 1e3，且至少有一种可行方案。

---

二、解题思路：

　　棋子是一行一行、一列一列的攻击的，所以我们可以一列一列的 dp 。

　　设 f[i][j] 表示前 i 列放 j 个棋子的方案数，s[i] 表示第 i 列的方格数。

　　容易得到状态转移方程：f[i][j]=f[i-1][j]+f[i-1][j-1]*(s[i]-(j-1))。

　　其实很好理解：

　　第 i 列不放棋子的情况下，f[i][j]+=f[i-1][j]。这种情况不用说了吧？

　　第 i 列要放棋子的情况下，f[i][j]+=f[i-1][j-1]*第 i 列可以放棋子的位置数量。

　　

　　关于第 i 列可以放棋子的位置数量：

　　一列一列地来看，我们 dp 方程一列本来就最多放一个，不用管。

　　一行一行地来看，f[i-1][j-1]表示前 i-1 行放了 j-1 个棋子。

　　一个棋子占据一行，其实就是第 i 列有 j-1 行不能放了。

　　那么还剩下 s[i]-(j-1) 个位置，f[i][j]+=f[i-1][j-1]*(s[i]-(j-1))。

　　但其实还有一个问题（困扰了我很久）：

　　如果 i-1 列有一些行是第 i 列没有的怎么办？例如最上面的图。

　　转移从左往右数的第 3 列时，第 2 列的方案里有一些是棋子放在了上面两行。

　　这些棋子显然不会占据第 3 列的空位，但状态转移方程会 默认占用第 3 行的空位，导致方案数减少。

　　

　　怎么解决呢？

　　显然只有 s[i-1]>s[i] 才会出现这种问题，所以从右往左倒着转移就好了！

---

三、完整代码：

 1 #include<iostream>
 2 #define N 2010
 3 #define M 100003
 4 using namespace std;
 5 int a,b,c,d,k;
 6 int s[N],f[N][N];
 7 int main()
 8 {
 9     cin>>a>>b>>c>>d>>k;
10     for(int i=1;i<=a;i++)    s[i+c]+=b;
11     for(int i=0;i<=a+c;i++)    s[i]+=d+1,f[i][0]=1;
12     for(int i=1;i<=a+c;i++)
13         for(int j=1;j<=k;j++)
14             f[i][j]=(f[i-1][j-1]*(s[i]-j)+f[i-1][j])%M;
15     cout<<f[a+c][k]<<'\n';
16     return 0;
17 }

---

四、写题心得：

　　好了，总算把这题想明白了，状态转移方程也是自己推的。很好，加油！