css3 matrix 2D矩阵和canvas transform 2D矩阵

一看到“2D矩阵”这个高大上的名词，有的同学可能会有种畏惧感，“矩阵”，看起来好高深的样子，我还是看点简单的吧。其实本文就很简单，你只需要有一点点css3 transform的基础就好。

没有前戏，直奔主题

2D矩阵指的是元素在2D平面内发生诸如缩放、平移、旋转、拉伸四种变化，在css3中对应4个方法分别是scale()、translate()、rotate()和skew()，可以说这4个方法是css3矩阵matrix的快捷方式，因为这4个方法本质都是由matrix实现的。类似地，在canvas中，与前3种变化对应的3个方法分别是scale()、translate()、rotate()，canvas对象没有skew()方法。css3中的矩阵和canvas矩阵原理是相通的，所以这里只说css3的矩阵matrix，两者有一些区别，后面会说。

matrix方法有六个参数matrix(a, b, c, d, x, y)，六个参数默认值是matrix(1, 0, 0, 1, 0, 0)，这六个参数分别控制不同的变换

a 水平缩放

b 水平拉伸

c 垂直拉伸

d 垂直缩放

x 水平位移

y 垂直位移

可以运行下面的demo，改动对应的参数查看效果

<style>
.con{margin: 0 auto; text-align: center;padding:4px 0;}
#box{width: 300px;height: 100px; font-size: 30px; border: 1px solid red;margin: 100px auto;}
</style>
<div class="con">
matrix(<input id="data" onblur='javascript:var oInput = document.getElementById("data"),
box = document.getElementById("box");box.style.transform = "matrix("+oInput.value+")";' type="text" value="1,0,0,1,0,0" />)失去焦点查看变化
</div>
<p class="con">还可以设置负数的哟</p>
<div id="box">matrix 2D矩阵</div>

执行

如果把以上css3的4个方法还原成矩阵的写法，它们是这样的：

• 缩放：scale(sx, sy) 等同于 matrix(sx, 0, 0, sy, 0, 0);
• 平移：translate(tx, ty) 等同于 matrix(1, 0, 0, 1, tx, ty);
• 旋转：rotate(deg) 等同于 matrix(cos(deg), sin(deg), -sin(deg), cos(deg), 0, 0);
• 拉伸：skew(degx, degy) 等同于 matrix(1, tan(degy), tan(degx), 1, 0, 0);

一目了然，matrix原始写法看起来更复杂一些，大家一般使用左边的快捷方式就好了。

计算变换后的transform-origin

其实矩阵基本上就上面这些内容，网上大部分介绍矩阵的教程一般都会搬出下面这张图来吓唬人

图1：

a c e分别和x y 1相乘并相加得出结果x' = ax + cy + e；

b d f分别和x y 1相乘并相加得出结果y' = bx + dy + f；

其中的x y是元素变换之前的中心点，即transform-origin的值，x' y'是元素变换之后的transform-origin值。

假设一个元素的中心点为100,100，将该元素向右平移200px，向下平移100px后，中心点坐标为:

x' =  ax + cy + e = 1*100 + 0*100 + 200 = 300

y' = 0*100 + 1*100 + 100 = 200

平移后的中心点坐标为300，200

图2：

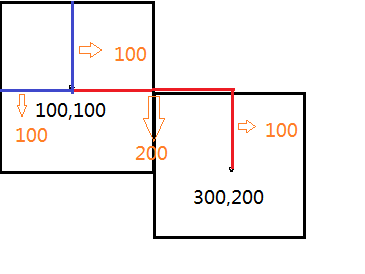
图1的作用仅仅是告诉我们如何计算元素变换后的中心点，没什么特别的。

css3 matrix和canvas transform的区别

大家都知道css3 transform-origin默认是元素的中点，css3旋转就是绕着这个点转动，而canvas的transform的rotate方法是默认绕着canvas的原点（即左上角）旋转。

<style>
.demo{width: 200px; height: 200px;background-color: blue; float: left; margin-right: 50px;transition:all 1s; font-size:50px;}
.demo:hover{transform:rotate(360deg);}
</style>
<div class="demo">鼠标滑过查看效果</div>
<canvas id="canvas2" style="background:red;" width="400" height="400"></canvas>
<script>

var canvas = document.getElementById("canvas2"),
ctx = canvas.getContext("2d"),
deg = 0;
setInterval(function(){
deg++;
deg > 360 && 0;
ctx.clearRect(0,0,400,400);
drewRect();
},50)
function drewRect(){
ctx.save();
ctx.beginPath();
// ctx平移后canvas的原点变为150,150
ctx.translate(150,150);
ctx.transform(Math.cos(deg), Math.sin(deg), -Math.sin(deg), Math.cos(deg), 0, 0);
ctx.fillRect(0,0,100,100);
ctx.restore();
}
</script>

执行

OK，以上就是2D矩阵的全部内容，对文中的公式建议自己做个demo测试一下以加深印象，否则看完一会准会忘记。

水平有限，有疏漏之处欢迎交流。

by：王美建 from http://www.cnblogs.com/wangmeijian/p/4713722.html转载注明出处。