Bzoj5251 线段树+贪心

Bzoj5251 线段树+贪心

记录本蒟蒻省选后的第一篇题解!
国际惯例的题面: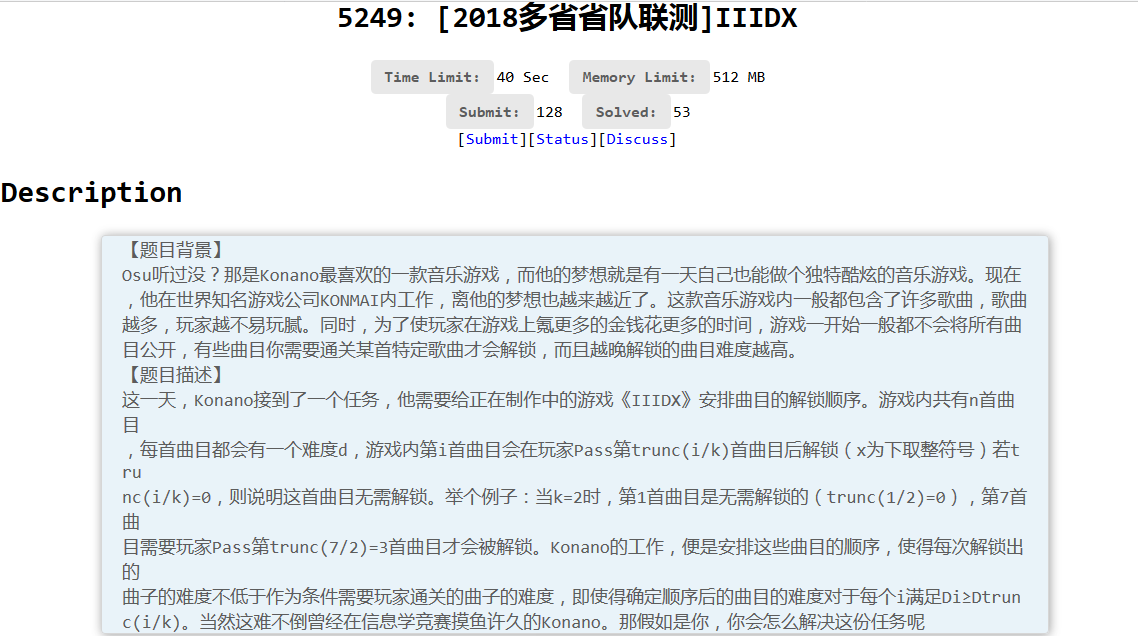

首先这个东西显然是一棵树。
如果我们把数值排序，并建立这棵树的dfs序，显然dfs序上的一个区间对应数值的一个区间，且根为数值区间左端点。
如果你这样想，恭喜你能获得50分，如果记得加了eps会获得55~60分。
因为当数值可以相同的时候，这个贪心是存在反例的。
考虑10个点的二叉堆，9个1一个2，显然2应该在位置6，而这样跑出来2会在位置10！
因为可能一个子树的数值是不连续的，我们可以在把根节点的位置减小为相同数值的左一个的时候，把这个区间的一个值分给别的子树。
考虑修正贪心。
我们离散化序列，记录每个值出现次数。
然后我们令f[i]表示>=i的数的个数。
先统计出子树size，考虑bfs遍历整个子树。
这样我们子树的根节点x要选择的就是满足f[1,i]均>=siz[x]的最大的i，我们令ans[x]=i。
之后我们需要让f[1,i]减去siz[x]，为了给这个子树预留位置。
当然，在遍历到一个节点的时候需要把为他的父亲预留的size加回去，也就是说，让f[1,ans[fa[x]]]加上siz[fa[x]]-1。
这个线段树二分怎么实现？由于这个序列不单调，我们维护区间min，如果左区间的min>=siz[x]的话就去右区间查询。
最后特判当前的点能否选择即可。
(考试的时候想到了线段树，但是非得用dfs序列遍历，怎么也弄不对......)

注意这题BZOJ卡eps!!!!!

代码:

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #define debug cout
 using namespace std;
 const int maxn=5e5+1e2;
 const double eps=1e-;

 int in[maxn],srt[maxn],siz[maxn],len;
 int ans[maxn],fa[maxn],ts[maxn],vis[maxn];
 int n;

 struct SegmentTree {
     int l[maxn<<],r[maxn<<],lson[maxn<<],rson[maxn<<],lazy[maxn<<],mi[maxn<<],cnt;
     inline void build(int pos,int ll,int rr) {
         l[pos] = ll , r[pos] = rr;
         if( ll == rr ) return;
         const int mid = ( ll + rr ) >> ;
         build(lson[pos]=++cnt,ll,mid) , build(rson[pos]=++cnt,mid+,rr);
     }
     inline void apply(int pos,int delta) {
         mi[pos] += delta , lazy[pos] += delta;
     }
     inline void push(int pos) {
         if( !lazy[pos] || l[pos] == r[pos] ) return;
         apply(lson[pos],lazy[pos]) , apply(rson[pos],lazy[pos]) , lazy[pos] = ;
     }
     inline void maintain(int pos) {
         if( l[pos] == r[pos] ) return;
         mi[pos] = min( mi[lson[pos]] , mi[rson[pos]] );
     }
     inline void update(int pos,int ll,int rr,int delta) {
         if( r[pos] < ll || rr < l[pos] ) return;
         if( ll <= l[pos] && r[pos] <= rr ) return apply(pos,delta);
         push(pos);
         update(lson[pos],ll,rr,delta) , update(rson[pos],ll,rr,delta);
         maintain(pos);
     }
     inline int query(int pos,int lim) {
         if( l[pos] == r[pos] ) return mi[pos] >= lim ? l[pos]  : l[pos] - ;
         push(pos);
         if( mi[lson[pos]] >= lim ) return query(rson[pos],lim);
         else return query(lson[pos],lim);
     }
 }segt;

 inline void getseq() {
     sort(in+,in++n);
     srt[len=] = in[] , siz[] = ;
     for(int i=;i<=n;i++) {
         if( in[i] != in[i-] ) srt[++len] = in[i];
         ++siz[len];
     }
     segt.build(segt.cnt=,,len);
     for(int i=;i<=len;i++) segt.update(,,i,siz[i]);
 }

 inline void calcpoint(int x) {
     if( fa[x] && !vis[fa[x]] ) segt.update(,,ans[fa[x]],ts[fa[x]]-) , vis[fa[x]] = ;
     int fd = segt.query(,ts[x]); ans[x] = fd;
     segt.update(,,fd,-ts[x]);
 }

 int main() {
     static double k;
     scanf("%d%lf",&n,&k);
     for(int i=;i<=n;i++) scanf("%d",in+i) , fa[i] = (int) ( (double) i / k + eps ) , ts[i] = ;
     getseq();
     for(int i=n;i;i--) if( fa[i] ) ts[fa[i]] += ts[i];
     for(int i=;i<=n;i++) calcpoint(i);
     for(int i=;i<=n;i++) printf("%d%c",srt[ans[i]],i!=n?' ':'\n');
     return ;
 }