运输问题中产销不平衡问题（表上作业法和LINGO方法）

对于产销不平衡问题有两种情况：

　　供大于求（产大于销）→增加虚拟销地

　　供不应求（产小于销）→增加虚拟产地

例如以下例题：

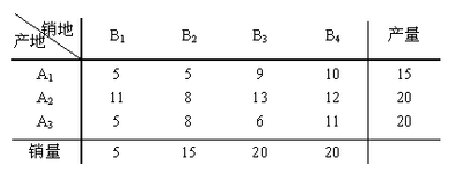
这个题中，总产量为55，总销量为60，故而我们知道这个问题属于供不应求。

1.这个问题可以采用笔算的方式：

　　表上作业法

　　　　↓

　　得到初始方案

　　　　↓

　　检验基变量个数是否为m+n-1个，若不是，则说明初始解退化，需要不足基变量个数（如填写一个数字同时满足了一厂一商，则需在同行或同列中填写一个数字0，以保证恰好有m+n-1个数字）【注意：基可行解中不能有某个基变量独占一行一列】

　　　　↓计算位势值（*）

　　基于基变量的c_ij计算出v_j和u_i，根据公式：c_ij=v_j+u_i,可以令v₁=0(随意设置)

　　　　↓

　　基于非基变量的表格，计算出非基变量检验数，σ_ij=c_ij-（v_j+u_i）。

　　　　↓若σ_{ij全非负，则说明初始方案为最优方案，从而计算出运输费用。}

　　若存在σ_ij < 0 ，则说明初始方案不是最优方案，需要进行调整。首先在作业表上以xij为起始变量作出闭回路（其余顶点均为基变量，回路中每行每列只有两个变量）, 并求出调整量 ε: ε=min{该闭回路中偶数次顶点调运量xij}。

　　　　　↓

　　以x_ij为起始变量_，其余顶点为基变量的闭回路，1.闭回路之外的变量调运量不变，2.闭回路上：偶数号顶点的调运量减去ε， 奇数号顶点的调运量加上ε。（*）

　　　　　↓

　　重复计算（*）之间的步骤，直到非基变量检验数全部为非负时，方案为最优方案。

2.LINGO计算最优方案

 sets:
 supplys/../: produce;
 demands/../: sell;
 links(supplys, demands): c, x;
 endsets
 data:
 produce = ,,;
 sell = ,,,;
 c =    

        ;
 enddata
 min = @sum(links(i,j): c(i,j) * x(i,j));
 @for(supplys(i): @sum(demands(j): x(i,j)) = produce(i));
 @for(demands(j): @sum(supplys(i): x(i,j)) <= sell(j));

运行结果如下：

  Global optimal solution found.
  Objective value:                              415.0000
  Infeasibilities:                              0.000000
  Total solver iterations:                             

  Model Class:                                        LP

  Total variables:
  Nonlinear variables:
  Integer variables:                    

  Total constraints:
  Nonlinear constraints:                

  Total nonzeros:
  Nonlinear nonzeros:                   

                                Variable           Value        Reduced Cost
                             PRODUCE( )        15.00000            0.000000
                             PRODUCE( )        20.00000            0.000000
                             PRODUCE( )        20.00000            0.000000
                                SELL( )        5.000000            0.000000
                                SELL( )        15.00000            0.000000
                                SELL( )        20.00000            0.000000
                                SELL( )        20.00000            0.000000
                                C( , )        5.000000            0.000000
                                C( , )        5.000000            0.000000
                                C( , )        9.000000            0.000000
                                C( , )        10.00000            0.000000
                                C( , )        11.00000            0.000000
                                C( , )        8.000000            0.000000
                                C( , )        13.00000            0.000000
                                C( , )        12.00000            0.000000
                                C( , )        5.000000            0.000000
                                C( , )        8.000000            0.000000
                                C( , )        6.000000            0.000000
                                C( , )        11.00000            0.000000
                                X( , )        5.000000            0.000000
                                X( , )        10.00000            0.000000
                                X( , )        0.000000            0.000000
                                X( , )        0.000000            1.000000
                                X( , )        0.000000            3.000000
                                X( , )        5.000000            0.000000
                                X( , )        0.000000            1.000000
                                X( , )        15.00000            0.000000
                                X( , )        0.000000            3.000000
                                X( , )        0.000000            6.000000
                                X( , )        20.00000            0.000000
                                X( , )        0.000000            5.000000

                                     Row    Slack or Surplus      Dual Price
                                               415.0000           -1.000000
                                               0.000000           -9.000000
                                               0.000000           -12.00000
                                               0.000000           -6.000000
                                               0.000000            4.000000
                                               0.000000            4.000000
                                               0.000000            0.000000
                                               5.000000            0.000000

由此可知：

最优方案为：

　　　　　　

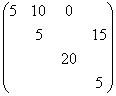
运输费用为 415 。

本篇文章为原创，转载请说明出处。