HDU1588

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1588

题目大意：g（i）= k * i + b. 给定 k 和 b，求0 <= i < n 的斐波那契数 F（g（i））的和模1,000,000,000.

解题思路：

　　矩阵快速幂再加上二分矩阵公式。

　　首先，我们需要认识到的一点是：对于这种求斐波那契数的题，很多都是用矩阵快速幂根据如下公式来计算的。

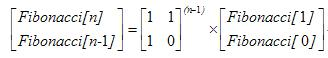
　　我们在此把中间那个0\1矩阵设为A。要求 The_Sum_of_F（g（i）），只需求出 A^(g(0)-1) + A^(g(1)-1) + A^(g(2)-1) + ... + A^(g(n-1)-1) = A^(b-1) + A^(i+b-1) + A^(2*i+b-1) + ...... = A^(b-1) + A^(b-1) * (A^i + A^(2*i) + A^(3*i) + ......). A^(b-1) = Ab, A^i = Ai,这些都可以用矩阵快速幂求出来。那么式子就变成：Ab＋Ab * (Ai + Ai^2 + Ai^3 + ......).加粗的那部分用二分矩阵公式递归求出。下面给出二分矩阵公式的一个例子：A^1+A^2+A^3+A^4+A^5+A^6=(A^1+A^2+A^3)+A^3(A^1+A^2+A^3)。

AC代码：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 using namespace std;
 typedef long long ll;
 const int maxn = ;
 struct Matrix {
     ll mat[][];
 };
 Matrix E;
 ll M;
 Matrix Multiply(Matrix x,Matrix y) {
     Matrix temp;
     memset(temp.mat, , sizeof(temp.mat));
     for (int i = ; i < ; i++)
         for (int j = ; j < ; j++) {
             for (int k = ; k < ; k++) {
                 temp.mat[i][j] += (x.mat[i][k] * y.mat[k][j]%M);
                 temp.mat[i][j]%=M;
             }
         }
     return temp;
 }
 Matrix Add(Matrix x,Matrix y){
     Matrix temp;
     for (int i = ; i < ; i++){
         for (int j = ; j < ; j++) {
             temp.mat[i][j]=(x.mat[i][j]+y.mat[i][j])%M;
         }
     }
     return temp;
 }
 Matrix Fast_Power(Matrix a, int m) {        //求a的m次幂
     Matrix res;
     memset(res.mat, , sizeof(res.mat));
     for (int i = ; i < ; i++)        res.mat[i][i] = ;
     while (m) {
         if (m & )    res = Multiply(res, a);
         m >>= ;
         a = Multiply(a, a);
     }
     return res;
 }
 Matrix Binary_add(Matrix B,int t){
     if(t==)    return B;
     if(t%==){
         return Add(Multiply(Binary_add(B,(t-)/),Add(E,Fast_Power(B,(t-)/))),Fast_Power(B,t));
     }
     else
         return Multiply(Binary_add(B,t/),Add(E,Fast_Power(B,t/)));
 }
 int main()
 {
     E.mat[][]=E.mat[][]=;
     E.mat[][]=E.mat[][]=;
     Matrix A;
     A.mat[][]=A.mat[][]=A.mat[][]=;
     A.mat[][]=;
     ll k,b,n,t;
     while(scanf("%lld%lld%lld%lld",&k,&b,&n,&M)==){
         Matrix Ab,B,ans;
         B=Fast_Power(A,k);
         Ab=Fast_Power(A,b);
         ans=Add(Ab,Multiply(Ab,Binary_add(B,n-)));
         printf("%lld\n",ans.mat[][]);
     }
     return ;
 }