Multism的简单使用(半加器和全加器)




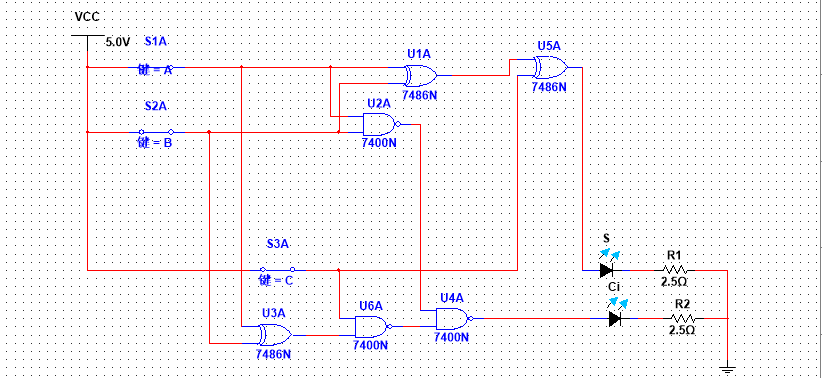
Multism的简单使用(半加器和全加器)的更多相关文章
- 2.计算机组成-数字逻辑电路 门电路与半加器 异或运算半加器 全加器组成 全加器结构 反馈电路 振荡器 存储 D T 触发器 循环移位 计数器 寄存器 传输门电路 译码器 晶体管 sram rom 微处理 计算机
现代计算机的各个部件到底是如何通过逻辑电路构成的呢 半加器 我们说过了门电路 看似简单的三种门电路却是组成了整个逻辑电路的根基 真值表--其实就是根据输入输出状态枚举罗列出来的所有可能 比如有一台 ...
- OpenRisc-42-or1200的ALU模块分析
引言 computer(计算机),顾名思义,就是用来compute(计算)的.计算机体系结构在上世纪五六十年代的时候,主要就是研究如何设计运算部件,就是想办法用最少的元器件(那时元器件很贵),最快的速 ...
- FPGA学习笔记(三)—— 数字逻辑设计基础(抽象的艺术)
FPGA设计的是数字逻辑,在开始用HDL设计之前,需要先了解一下基本的数字逻辑设计-- 一门抽象的艺术. 现实世界是一个模拟的世界,有很多模拟量,比如温度,声音······都是模拟信号,通过对模拟信号 ...
- CPU怎么计算1+1----CPU计算的电路基础
从<十进制和二进制的运算---我所理解到的人类的运算的本质>这里我们知道,人类进行运算的本质是查表,并且我们存储的表是有限的.那么计算机是怎进行四则运算的呢,也是查表吗,肯定不是,今天,我 ...
- Cracking Digital VLSI Verification Interview 第四章
目录 Hardware Description Languages Verilog SystemVerilog 对Cracking Digital VLSI Verification Intervie ...
- 逻辑式编程语言极简实现(使用C#) - 1. 逻辑式编程语言介绍
相信很多朋友对于逻辑式编程语言,都有一种最熟悉的陌生人的感觉.一方面,平时在书籍.在资讯网站,偶尔能看到一些吹嘘逻辑式编程的话语.但另一方面,也没见过周围有人真正用到它(除了SQL). 遥记当时看&l ...
- 【FPGA学习】Verilog之加法器
在fpga工程应用设计中,随处可见加法器,乘法器等等.现在将一些常用模块和心得体会先记录下来,以便日后使用. 一位半加器: module halfadder(cout,sum,a,b); output ...
- FPGA学习笔记(四)——Verilog基本语法
###### [该随笔部分内容转载自小梅哥] ######### 组合逻辑: 多路选择器.加法器.译码器.乘法器 时序逻辑: 计数器.分频器.定时器.移位寄存器 一.Verilog文件的基 ...
- Verilog 加法器和减法器(2)
类似半加器和全加器,也有半减器和全减器. 半减器只考虑当前两位二进制数相减,输出为差以及是否向高位借位,而全减器还要考虑当前位的低位是否曾有借位.它们的真值表如下: 对半减器,diff = x ^y, ...
随机推荐
- 【多校】2019 Multi-University Training Contest 1官方题解
Blank 定义dp[i][j][k][t]dp[i][j][k][t]dp[i][j][k][t]代表填完前ttt个位置后,{0,1,2,3}\{0,1,2,3\}{0,1,2,3}这4个数字最后一 ...
- leetcode之820. 单词的压缩编码 | python极简实现字典树
题目 给定一个单词列表,我们将这个列表编码成一个索引字符串 S 与一个索引列表 A. 例如,如果这个列表是 ["time", "me", "bell& ...
- 翻转-Flip Columns For Maximum Number of Equal Rows
2020-02-20 11:00:06 问题描述: 问题求解: 翻转题一个常见的思路就是站在结束的状态来反推最初的状态,本题的解题思路就是站在结束的时候的状态来进行反推. 如果在最终的状态i-row是 ...
- 算法训练 瓷砖铺放 【递归】java
算法训练 瓷砖铺放 时间限制:1.0s 内存限制:512.0MB 锦囊1 锦囊2 锦囊3 问题描述 有一长度为N(1<=N<=10)的地板,给定两种不同瓷砖:一种长度为 ...
- sql-lib闯关1-10关
闯关之前我们需要搭建所需环境SQLi-Labs SQLi-Labs是一个专业的SQL注入练习平台,该平台包含了以下在测试场景中常见的注入类型: 1.报错注入(联合查询) 1)字符型 ...
- 【转】Standardization(标准化)和Normalization(归一化)的区别
Standardization(标准化)和Normalization(归一化)的区别 https://blog.csdn.net/Dhuang159/article/details/83627146 ...
- 在Ubuntu中安装OpenCV-Python | 三
在本教程中,我们将学习在Ubuntu System中设置OpenCV-Python.以下步骤针对Ubuntu 16.04和18.04(均为64位)进行了测试. 可以通过两种方式在Ubuntu中安装Op ...
- PyTorch Hub发布!一行代码调用最潮模型,图灵奖得主强推
为了调用各种经典机器学习模型,今后你不必重复造轮子了. 刚刚,Facebook宣布推出PyTorch Hub,一个包含计算机视觉.自然语言处理领域的诸多经典模型的聚合中心,让你调用起来更方便. 有多方 ...
- python中的函数及作用域的理解
内置函数 常用的几个内置函数 function des len 求长度 min 求最小值 max 求最大值 sorted 排序 reversed 反向 sum 求和 进制转换函数 function d ...
- jQuery学习笔记01
1.jQuery介绍 1.1什么是jQuery ? jQuery,顾名思义,也就是JavaScript和查询(Query),它就是辅助JavaScript开发的js类库. 1.2 jQuery核心思想 ...
