(1)常见O(n^2)排序算法解析

一、选择排序

1、原始数组

2、遍历数组找到最小值索引，并将最小值索引与当前遍历索引位置互换

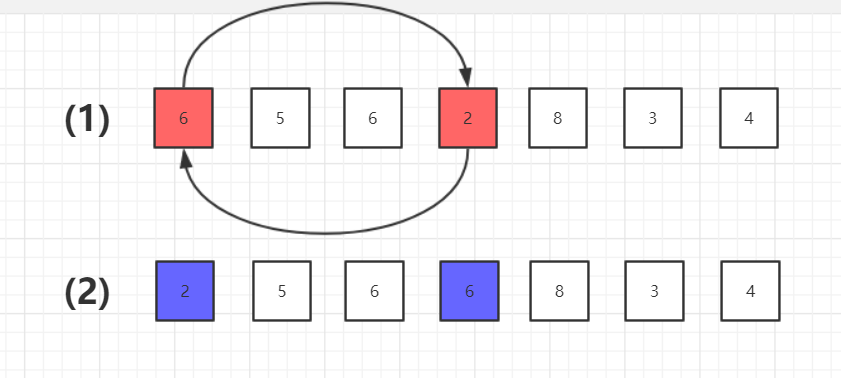
3、确定最小位置值，进行下一次遍历

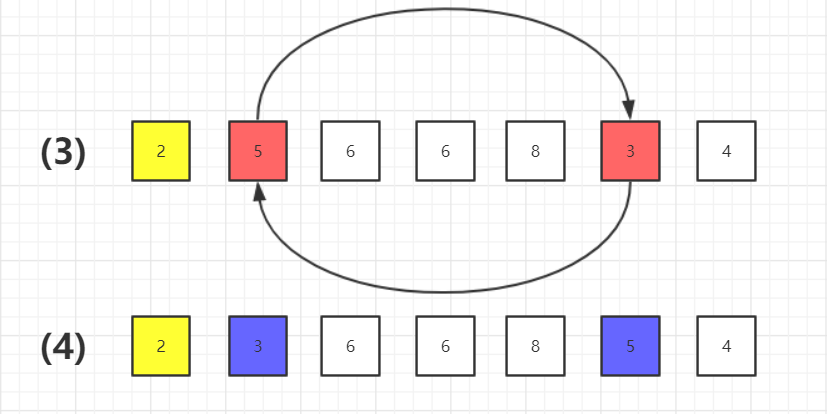
4、java代码实现

/**
  * author:sam
  * date:2018/1/26 14:11
  * describe:选择排序
  */
public void selectSort(int[] arr){
    for (int i = 0; i < arr.length; i++) {
        int minIndex = i;
        for (int j = i; j < arr.length; j++) {
            if(arr[minIndex] > arr[j])
                minIndex = j;
        }
        SortUtils.swap(arr,minIndex,i);
    }
}

二、插入排序

　　扑克牌整理牌型时思想，对于有序数组效率非常高。

1、以[0]位置数据为基点依次遍历后续数据

2、后续数据依次与当前数据进行比较，并将数据插入到合适位置

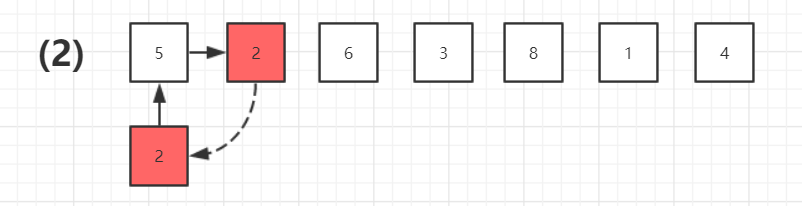
3、进行下依次插入

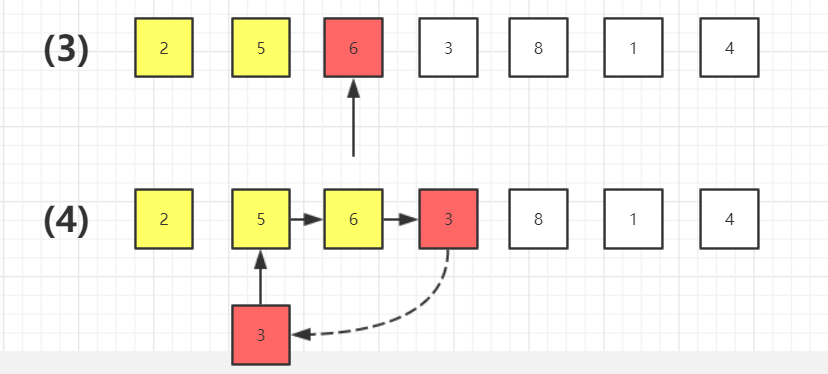
4、java代码实现

/**
  * author:sam
  * date:2018/3/7 10:49
  * describe:插入排序
  */
@Override
public void insertSort(int[] arr) {

    for (int i = 1; i < arr.length; i++) {
        for (int j = i; j > 0 && arr[j] < arr[j-1]; j--){
                SortUtils.swap(arr, j, j - 1);
        }
    }
}

5、插入排序优化

/**
  * author:sam
  * date:2018/3/7 12:21
  * describe:插入排序优化
  */
@Override
public void optimizeInsertSort(int[] arr) {

    for (int i = 1; i < arr.length; i++) {
        int e = arr[i];
        int index = i;
        for (int j = i; j > 0 && arr[j-1] > e; j--) {
            arr[j] = arr[j - 1];
            index = j - 1;
        }
        arr[index] = e;
    }

}

三、冒泡排序

1、冒泡排序
/**
  * author:sam
  * date:2018/3/7 14:37
  * describe:冒泡排序
  */
public void bubbleSort(int[] arr){

    for (int i = 0; i < arr.length; i++) {
        for (int j = 0; j < arr.length - i -1; j++) {
            if(arr[j] > arr[j+1]){
                SortUtils.swap(arr,j,j+1);
            }
        }
    }
}

2、冒泡排序优化
/**
  * author:sam
  * date:2018/3/7 14:49
  * describe:优化冒泡排序
  */
@Override
public void optimizeBubbleSort(int[] arr){
    /*boolean flag;
    int n = arr.length;
    do{
        flag = false;
        for (int i = 1; i < n; i++) {
            int j;
            if(arr[i] < arr[j = i-1]) {
                SortUtils.swap(arr, i, j);
                flag = true;
            }
        }
        n--;
    }while(flag);*/
   boolean flag;
   int n = arr.length;
   do{
       flag = false;
       int j;
       for (int i = 0; i < n - 1; i++) {
            if(arr[i] > arr[j = i + 1]){
                SortUtils.swap(arr,i,j);
                flag = true;
            }
       }
       n--;
   }while(flag);
}

四、shell排序