[BZOJ]1005 明明的烦恼(HNOI2008)

　　BZOJ的第一页果然还是很多裸题啊，小C陆续划水屯些板子。

Description

　　自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的树?

Input

　　第一行为N(0 < N < = 1000),接下来N行,第i+1行给出第i个节点的度数Di,如果对度数不要求,则输入-1.

Output

　　一个整数,表示不同的满足要求的树的个数,无解输出0.

Sample Input

　　3
　　1
　　-1
　　-1

Sample Output

　　2

HINT

　　两棵树分别为1-2-3;1-3-2.

Solution

　　碰见这种没有知识储备脑子里都没有想法的题，考场上还是保佑自己碰到一些自己学过的算法吧。

　　讲这道题之前先来说说prufer编码是什么：

　　　　①prufer编码是树的一种表示形式，不同的编码与不同的树形态一一对应；

　　　　　（不同的树形态指的是两棵树中至少有一条边连接的点不同）

　　　　②根据定理证明，n个点最多能构成(n-2)^n种不同的树形态。

　　　　　（至于为什么是这个式子看看接下来prufer编码是如何构造的就知道了）

　　　　③构造方法：

　　　　

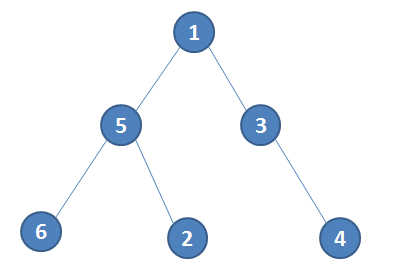
　　　　　如图所示，为一棵有6个结点的树，每次选出叶子节点中编号最小的一个，将与其相连的那个节点的标号加入数列，再将该叶子结点删去。直到树中剩下两个节点为止。

　　　　　所以上图的树的prufer编码就是：5 3 1 5（依次删去2 4 3 1）。

　　　　　显而易见，一棵节点数为n的树的prufer编码长度为n-2。

　　　　　由于prufer编码的每一位都有可能是1~n，不同的prufer编码有(n-2)^n种。

　　　　　所以根据第①条一一对应的性质，不同的树有(n-2)^n种。

　　利用prufer编码，我们可以轻易地解决这道题。

　　从prufer编码中，我们可以看出一棵树中所有点的度数，每个点的度数为它在prufer编码中出现的次数+1。

　　因此对于题目中规定度数的点，我们可以首先确定它们在prufer编码中的位置。

　　假设规定度数的点有p个，度数分别为a1、a2……ap。

　　那么把这p个点填进prufer编码的方案数是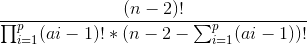。（排列组合、乘法原理瞎推）

　　那么prufer编码中剩下的空位有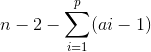个，未规定度数的节点有n-p个，所以方案数再乘上即可。

　　由于答案没有取模，所以要用到高精度乘/除单精度。

　　题目中所说的无解情况有3种：

　　　　①；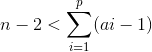

　　　　②；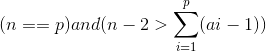

　　　　③。

　　时间复杂度写得不是太糟都能过，注意高精度数的位数。

#include <cstdio>
#include <algorithm>
#include <cstring>
#define ll long long
#define mod 1000000000
#define MS 354
using namespace std;
struct hp
{
    int len; ll ar[MS];
    friend hp operator/(const hp& a,int b)
    {
        register ll lt=;
        register int i;
        hp c;
        memset(&c,,sizeof(c));
        c.len=a.len;
        for (i=a.len-;i>=;--i)
        {
            lt=lt*mod+a.ar[i];
            c.ar[i]=lt/b; lt%=b;
        }
        if (!c.ar[c.len-]) --c.len;
        return c;
    }
    friend hp operator*(const hp& a,int b)
    {
        register int i,j;
        hp c;
        memset(&c,,sizeof(c));
        c.len=a.len;
        for (i=;i<a.len;++i)
        {
            c.ar[i]+=a.ar[i]*b;
            c.ar[i+]+=c.ar[i]/mod;
            c.ar[i]%=mod;
        }
        if (c.ar[c.len]) ++c.len;
        return c;
    }
}sum;
int n,rn,uk;

inline int read()
{
    int n=,f=; char c=getchar();
    while (c<'' || c>'') {if(c=='-')f=-; c=getchar();}
    while (c>='' && c<='') {n=n*+c-''; c=getchar();}
    return n*f;
}

int main()
{
    register int i,x;
    sum.ar[]=; sum.len=;
    n=read(); rn=n-;
    for (i=;i<=rn;++i) sum=sum*i;
    for (i=;i<=n;++i)
    {
        x=read()-;
        if (x>) {if (rn>=x) {for (rn-=x;x>=;--x) sum=sum/x;} else return *printf("");}
        else if (x==-) ++uk;
        else return *printf("");
    }
    if (rn&&!uk) return *printf("");
    for (i=;i<=rn;++i) sum=sum/i*uk;
    printf("%lld",sum.ar[sum.len-]);
    for (i=sum.len-;i>=;--i) printf("%09lld",sum.ar[i]);
}

Last Word

　　小C看到这道题的时候就觉得这肯定不是正常题，就是没有看过相关的东西死都做不出来的那种。

　　结果真的是这样。