通过内核修改centos密码
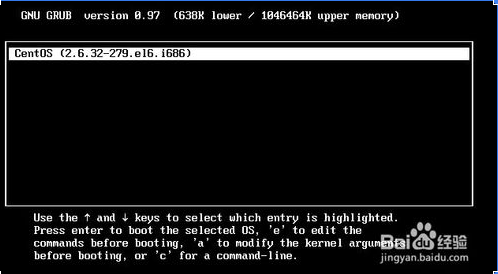
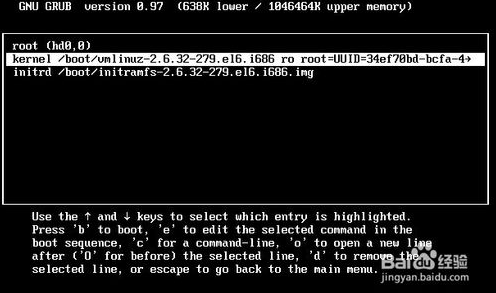
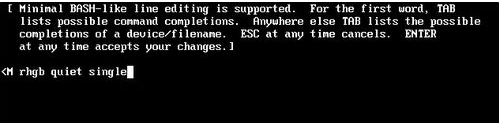

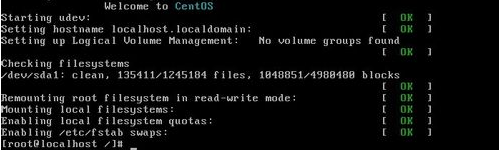
通过内核修改centos密码的更多相关文章
- CentOS单用户模式下修改ROOT密码和grub加密
Linux 系统处于正常状态时,服务器主机开机(或重新启动)后,能够由系统引导器程序自动引导 Linux 系统启动到多用户模式,并提供正常的网络服务.如果系统管理员需要进行系统维护或系统出现启动异常时 ...
- centos单用户模式:修改ROOT密码和grub加密
centos单用户模式:修改ROOT密码和grub加密 CentOSLinux网络应用配置管理应用服务器 Linux 系统处于正常状态时,服务器主机开机(或重新启动)后,能够由系统引导器程序自动引导 ...
- CentOS修改用户密码方法
CentOS修改用户密码方法 CentOS修改用户密码方法 1. 普通用户 a. 获取超级用户root权限 命令:su或者su -或者su - root b. passwd 用户名 2. 超级用户 a ...
- CentOS 单用户模式:修改Root密码和grub加密[转]
原文出处: http://zhengdl126.iteye.com/blog/430268 Linux 系统处于正常状态时,服务器主机开机(或重新启动)后,能够由系统引导器程序自动引导 Linux 系 ...
- RedHat/Centos修改root密码
Linux主机忘记密码,只要你能接触物理主机都可以修改root密码的! Redhat6.x 5.x / Centos6.x 5.x 01.开机-空格/enter 02.e-编辑模式 CentO ...
- CentOS 修改用户密码
CentOS 修改用户密码 1.普通用户 ①获取超级用户root权限 命令:su 或者 su- 或者 su -root ②输入命令: passwd 用户名 ③输入新密码 2.超级用户 ①打开syste ...
- CentOS 7修改管理员密码
之前安装CentOS 7的时候随便输入了一个密码,现在使用需要root权限,只能重置密码了.下面是处理方法:(进入单用户模式修改root密码为例) 在启动菜单中,按e编辑所选启动项 一页内容,感觉挺陌 ...
- CentOS 7 修改root 密码
环境: 1.重启系统在加载内核的地方按e,编辑启动脚本 2.将ro crashkernel = auto 所在地的 ro 替换为 rw init=/sysroot/bin/sh 3.修改完成后用Ctr ...
- Centos 7 忘记密码的情况下,修改root密码
应用场景 linux管理员忘记root密码,需要进行找回操作. 注意事项:本文基于centos7.4环境进行操作,由于centos的版本是有差异的,继续之前请确定好版本 操作步骤 一.重启系统,在开机 ...
随机推荐
- python3全栈开发-面向对象的三大特性(继承,多态,封装)之继承
一 .初识继承 1.什么是继承 继承是一种创建新类的方式,新建的类可以继承一个或多个父类(python支持多继承),父类又可称为基类或超类,新建的类称为派生类或子类. 特点: 子类会“”遗传”父类的属 ...
- 教你用命令行激活win10系统
对于笔者这样爱自己动手的电脑爱好者来说,当然会选择自己组装一台性价比高的台式电脑,一切都准备就绪了,系统也装好了,就差最后一步了--激活系统. 笔者真的很幸运,在网上找到了一些可以使用的密钥,我装的是 ...
- Maven 本地仓库明明有jar包,pom文件还是报错解决办法
方法一: 找到出错的jar包文件位置,删掉_maven.repositories文件 方法二: maven中的本地仓库的index索引没有更新导致 解决方案: 在eclipse中打开菜单 window ...
- mybatis学习成长之路(一)
从小白开始学习,希望自己学习的过程可以帮助更多需要的人,参考网址:https://www.cnblogs.com/ysocean/p/7237499.html 1.mybatis的jar包下载地址:h ...
- Lazy Loading | Explicit Loading | Eager Loading in EntityFramework and EntityFramework.Core
EntityFramework Eagerly Loading Eager loading is the process whereby a query for one type of entity ...
- [HNOI2011]任务调度
题目描述 有 N 个任务和两台机器 A 与 B.每个任务都需要既在机器 A 上执行,又在机器 B 上执行, 第 i 个任务需要在机器 A 上执行时间 Ai,且需要在机器 B 上执行时间 Bi.最终的目 ...
- codeforces868D Huge Strings
You are given n strings s1, s2, ..., sn consisting of characters 0 and 1. m operations are performed ...
- P3928 SAC E#1 - 一道简单题 Sequence2
题目背景 小强和阿米巴是好朋友. 题目描述 小强喜欢数列.有一天,他心血来潮,写下了三个长度均为n的数列. 阿米巴也很喜欢数列.但是他只喜欢其中一种,波动数列. 阿米巴把他的喜好告诉了小强.小强便打算 ...
- ●洛谷P2495 [SDOI2011]消耗战
题链: https://www.luogu.org/problemnew/show/P2495题解: 虚树入门,树形dp 推荐博客:http://blog.csdn.net/lych_cys/arti ...
- hdu 5521 最短路
Meeting Time Limit: 12000/6000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)Total ...
