class-提升方法Boosting
2 AdaBoost训练误差分析
3 AdaBoost algorithm 另外的解释
3.1 前向分步算法
3.2 前向分步算法与AdaBoost
4 提升树
4.1 提升树模型
4.2 梯度提升
Boosting在分类问题中,通过改变训练样本的权重,学习多个分类器,并将这些分类器进行线性组合,提高分类性能。AdaBoost最具代表性,由Freund和Schapire在1995年提出;Boost树在2000年由Friedman提出。
1 AdaBoost算法
基本思想:对于分类而言,给定一个训练样本集,求比较粗糙的分类规则(弱分类器)比强分类器容易得多。因此此方法就是从弱分类器出发,反复学习,得到一系列弱分类器(基本分类器),然后组合成一个强分类器。Boosting方法大多是改变训练数据的权值分布,针对不同训练数据分布调用弱分类器进行一系列学习的方法。如何改变训练数据的权值或概率分布?提高前一轮弱分类器错误分类的样本的权值,而降低正确分类样本的权值,这样错误分类的样本在本次弱分类器中就被更大的关注,一次分类问题就被一系列分类器分而治之。如何组合这一组弱分类器?——加权多数表决的方法,加大无误差率低的弱分类器的权值,减小误差率大的弱分类器的权值,让其在表决中起较小作用。
算法:


说明:
步骤一中,权值分布采取均匀分布得到权值向量D1,在原始数据上学习分类器;
步骤二中,m表示轮数,m=1表示第一轮学习过程。
(a)使用当前权值向量Dm加权训练集,学习基本分类器Gm(x)。
(b)计算基本分类器在加权训练集上的误分类率em,可以看出Gm(x)的分类误差率是误分类样本权重之和。
(c) Gm的系数就是在最终组合分类器所占的权重,表示此分类器的重要性。em小于1/2时,alpham>=0,随着误分类率的减小而增大,所以误分类率越小的基本分类器在最终分类器所起的作用越大。
(d)中更新权值分布,为下一轮做准备,其实yGm相乘是验证此个样本值分类的正确性,正确则同号,同号则为正,为正则指数部分为负数,就减少此样本值的分量,减少的多少由alpha决定。即
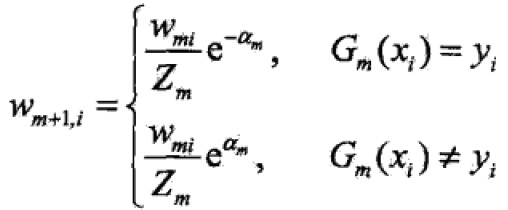
步骤三中,f(x)的线性组合实现了M个基本分类器的加权表决,系数alpha是基本分类器的重要性。注意这里的alpha之和不为1。f(x)的符号表示实例的类别,绝对值的大小表示分类的确信度。最终sign得到强分类器G(x)。
在具体执行过程中,可以每次都进行组合然后得到误分类点,直到误分类点为0为止或者达到m的最大值M为止。
2 AdaBoost训练误差分析
定理:训练误差的界:
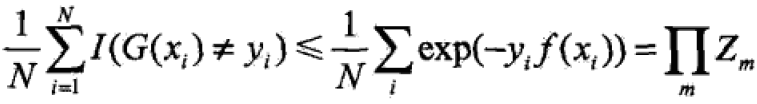
证明:

定理:二类分类的AdaBoost训练误差界:
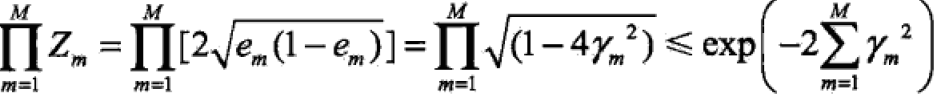 ,
,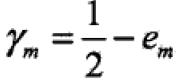
证明:
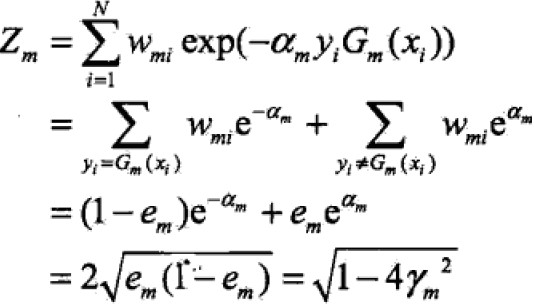

推论:
 表明AdaBoost误差界以指数速率下降。
表明AdaBoost误差界以指数速率下降。
注意:AdaBoost算法不需要知道下界γ,具有适应性adaptive Boosting
3 AdaBoost algorithm 另外的解释
这个解释是AdaBoost算法模型是加法模型,损失函数是指数函数,学习算法为前向分步算法时的二类分类学习方法。
3.1 前向分步算法
加法模型(additive model)
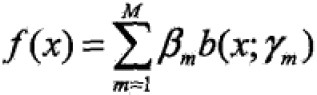
其中,b为基函数,γ为基函数的参数;β为基函数的系数;
给定训练集和损失函数L(y,f(x))条件下,学习加法模型f成为风险极小化或损失函数极小化的问题:
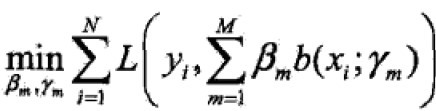
前向分步算法(forward stagewise algorithm)求解思路是:因为学习的模型是加法模型,如果能够从前向后,每一步只学习一个基函数及其系数,逐步逼近优化函数目标(上式),那么就可以简化优化的复杂度。因此,每步只需优化如下损失函数:
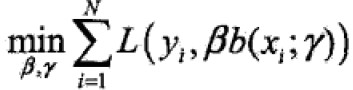
算法明细:

3.2 前向分步算法与AdaBoost
定理:AdaBoost算法是前向分步算法的特例,model为基本分类器组成的加法模型,损失函数是指数函数。
证明:根据算法流程对比二者并无区别,需要注意的是前向分步算法的损失函数是指数损失函数(exponential loss function)
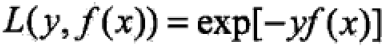

4 提升树
Boosting Tree被认为是统计学习中性能最好的方法之一,以分类树或回归树为基本分类器的提升方法。
4.1 提升树模型
提升方法实际上采用的是加法模型(基函数的线性组合)与前向分步算法。以决策树为基函数的提升方法称为提升树。对分类问题的决策树是二叉分类树,对回归问题的决策树是二叉回归树。基本分类器xv可以看做由一个根结点直接连接两个叶子结点的简单决策树,即决策树桩(decision stump)。提升树模型可以表示为决策树的加法模型:
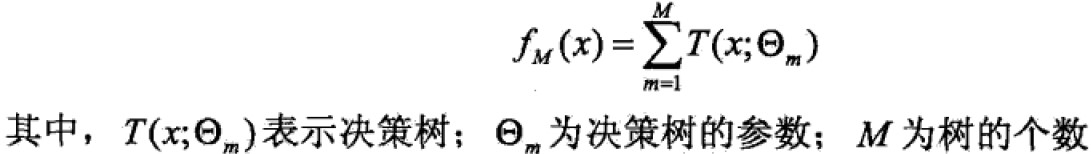
提升算法采用前向分步算法,首先确定初始提升树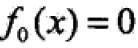 ,则第m步的模型是
,则第m步的模型是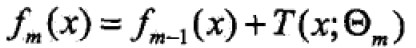 ;
;
经验最小化函数: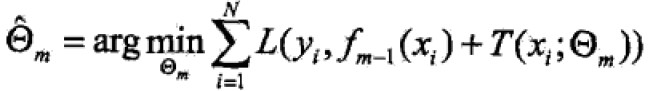 ,m-1表示当前树,经验最小化函数可以确定下一个树的决策参数。
,m-1表示当前树,经验最小化函数可以确定下一个树的决策参数。
不同问题的提升树学习算法,主要区别是使用的损失函数不同(回归问题:平方误差损失函数;分类问题指数损失函数)。
回归问题
已知训练集T={(x1,x2),…(xN,yN)},x属于Rn,y属于R,如果将输入空间划分为J个互不相交的区域R1,…,RJ,并且在每个区域上确定输出常量cj,树可表示为
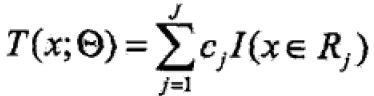
其中,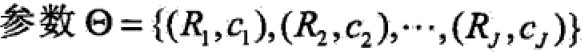 表示树的区域划分和各区域上常数(类)。J是回归树的复杂度即叶子结点个数。
表示树的区域划分和各区域上常数(类)。J是回归树的复杂度即叶子结点个数。
回归提升树使用前向分步算法:
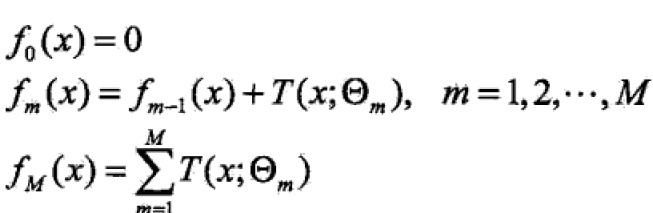
前向分步算法第m步,给定当前模型fm-1,需求: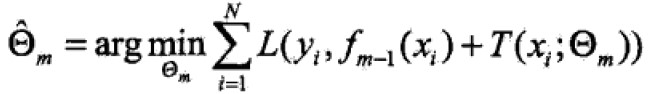 。
。
当采用平方误差损失函数时, 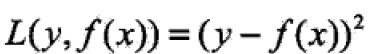
代入得:
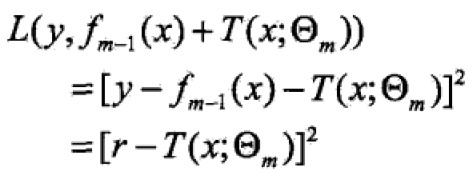
这里,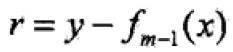 是当前模型拟合数据的残差(residual)
是当前模型拟合数据的残差(residual)
回归树算法:

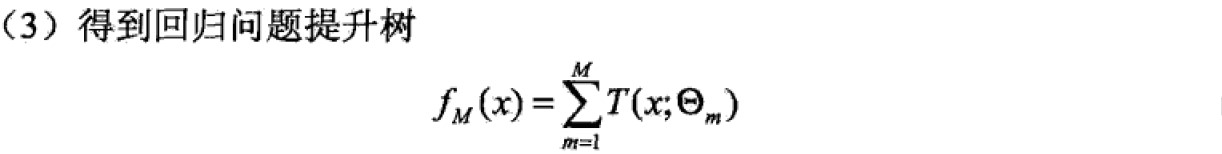
4.2 梯度提升
当损失函数不是平方误差函数或者指数函数时,优化并不简单,故提出梯度提升(gradient Boosting)算法,关键是利用损失函数的负梯度在当前模型的值
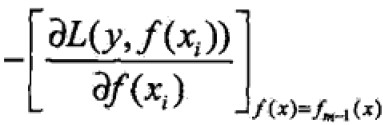 作为回归问题中残差的近似值拟合回归树。
作为回归问题中残差的近似值拟合回归树。
梯度提升算法:

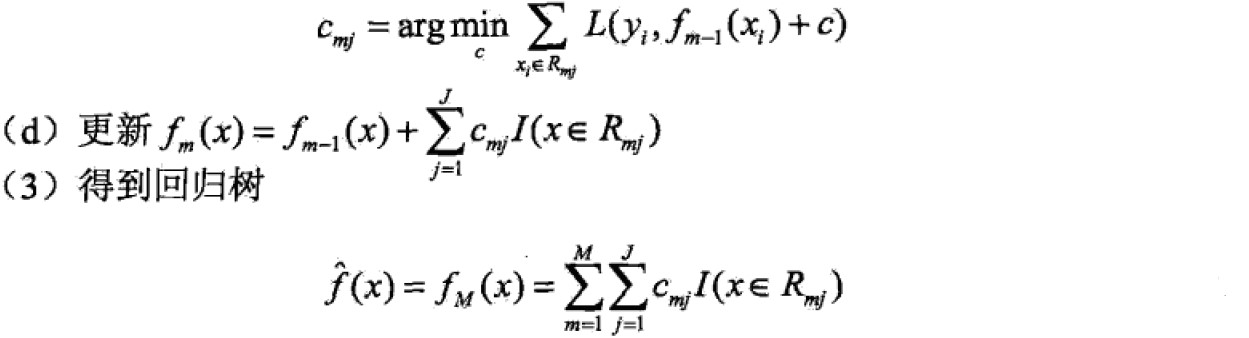
class-提升方法Boosting的更多相关文章
- 提升方法(boosting)详解
提升方法(boosting)详解 提升方法(boosting)是一种常用的统计学习方法,应用广泛且有效.在分类问题中,它通过改变训练样本的权重,学习多个分类器,并将这些分类器进行线性组合,提高分类的性 ...
- Boosting(提升方法)之GBDT
一.GBDT的通俗理解 提升方法采用的是加法模型和前向分步算法来解决分类和回归问题,而以决策树作为基函数的提升方法称为提升树(boosting tree).GBDT(Gradient Boosting ...
- Boosting(提升方法)之AdaBoost
集成学习(ensemble learning)通过构建并结合多个个体学习器来完成学习任务,也被称为基于委员会的学习. 集成学习构建多个个体学习器时分两种情况:一种情况是所有的个体学习器都是同一种类型的 ...
- 组合方法(ensemble method) 与adaboost提升方法
组合方法: 我们分类中用到非常多经典分类算法如:SVM.logistic 等,我们非常自然的想到一个方法.我们是否可以整合多个算法优势到解决某一个特定分类问题中去,答案是肯定的! 通过聚合多个分类器的 ...
- js 变量提升+方法提升
<!DOCTYPE html> <html> <head lang="en"> <meta charset="UTF-8&quo ...
- 机器学习理论提升方法AdaBoost算法第一卷
AdaBoost算法内容来自<统计学习与方法>李航,<机器学习>周志华,以及<机器学习实战>Peter HarringTon,相互学习,不足之处请大家多多指教! 提 ...
- 统计学习方法c++实现之七 提升方法--AdaBoost
提升方法--AdaBoost 前言 AdaBoost是最经典的提升方法,所谓的提升方法就是一系列弱分类器(分类效果只比随机预测好一点)经过组合提升最后的预测效果.而AdaBoost提升方法是在每次训练 ...
- 提升方法-AdaBoost
提升方法通过改变训练样本的权重,学习多个分类器(弱分类器/基分类器)并将这些分类器进行线性组合,提高分类的性能. AdaBoost算法的特点是不改变所给的训练数据,而不断改变训练数据权值的分布,使得训 ...
- 机器学习——提升方法AdaBoost算法,推导过程
0提升的基本方法 对于分类的问题,给定一个训练样本集,求比较粗糙的分类规则(弱分类器)要比求精确的分类的分类规则(强分类器)容易的多.提升的方法就是从弱分类器算法出发,反复学习,得到一系列弱分类器(又 ...
随机推荐
- 洛谷 [P4011] 孤岛营救问题
状压+BFS 通过观察数据范围可知,我们应该状压钥匙种类,直接BFS即可 注意,一个点处可能不知有一把钥匙 #include <iostream> #include <cstdio& ...
- python学习1:程序元素和基本使用方法(跟随mooc学习)
程序元素: 注释,缩进,变量,常量,表达式 输入,输出,分支,循环 示例程序,温度转换程序: #TempConvert.pyval=input("请输入带温度表示符号发温度值(例如:32C) ...
- LeetCode - 626. Exchange Seats
Mary is a teacher in a middle school and she has a table seat storing students' names and their corr ...
- Project support for both iOS 6 and iOS 7
原文:https://developer.apple.com/library/ios/documentation/UserExperience/Conceptual/TransitionGuide/S ...
- CSS3总结(干货)
1.css3中好用的选择器 :target //突出显示活动的HTML锚 ::after / ::before{content:" ";} //content必须有,若无内容,用空 ...
- [NOIP]2016天天爱跑步
[NOIP]2016天天爱跑步 标签: LCA 树上差分 NOIP Description 小C同学认为跑步非常有趣,于是决定制作一款叫做<天天爱跑步>的游戏.<天天爱跑步>是 ...
- Java经典编程题50道之三十九
写一个函数,求一个字符串的长度,在main函数中输入字符串,并输出其长度. public class Example39 { public static void main(String[] a ...
- 从flexible.js引入高德地图谈起的移动端适配
曾几何时,前端还仅仅是PC端的.随着移动时代的兴起,h5及css3的推陈出新.前端的领域慢慢的由传统的pc端转入了移动端,这也导致了前端这一职业在风口的一段时间出尽了风头. 从开始的惶恐和无从下手,慢 ...
- npm注意事项(附带Vue-cli安装)
下载完nodeJS后,可选择更改配置目录 1.npm config set prefix "D:\node\node-global"<!--配置全局安装目录--> 2. ...
- eclipse中创建一个maven项目
1.什么是Maven Apache Maven 是一个项目管理和整合工具.基于工程对象模型(POM)的概念,通过一个中央信息管理模块,Maven 能够管理项目的构建.报告和文档. Maven工程结构和 ...
