矩阵分解ALS方法

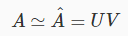
目标函数

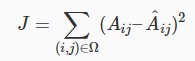
优化目标函数

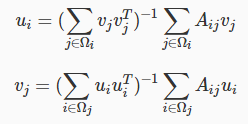
利用坐标下降法，依次更新u和v的值。u和v的先后顺序无所谓，只要保证两者是交替更新的就好。这种方法又称为alternating least squares（ALS）。

增加偏置项

在行和列都增加一个常数项，去除每个用户的个体影响。

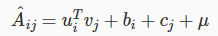
更新的公式修正为

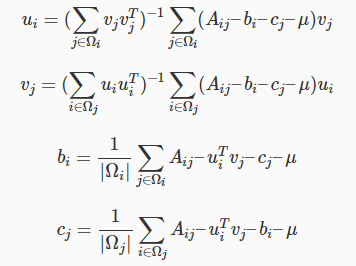
增加正则项

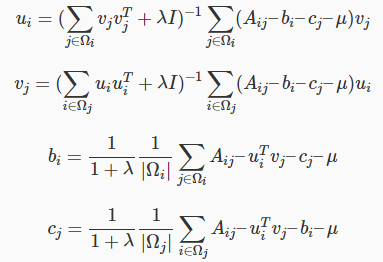
实现代码

## 初始化矩阵
U = np.random.randn(M, K) / K
V = np.random.randn(K, N) / K
B = np.zeros(M)
C = np.zeros(N)

## 迭代T步，每一步依次更新B、U、C、V矩阵
for t in xrange(T):

  # update B
  for i in xrange(M):
  if i in ratings_by_i:
    accum = 0
    for j, r in ratings_by_i[i]:
      accum += (r - U[i,:].dot(V[:,j]) - C[j] - mu)
    B[i] = accum / (1 + reg) / len(ratings_by_i[i])

  # update U
  for i in xrange(M):
    if i in ratings_by_i:
      matrix = np.zeros((K, K)) + reg*np.eye(K)
      vector = np.zeros(K)
      for j, r in ratings_by_i[i]:
        matrix += np.outer(V[:,j], V[:,j])
        vector += (r - B[i] - C[j] - mu)*V[:,j]
      U[i,:] = np.linalg.solve(matrix, vector)

  # update C
  for j in xrange(N):
    if j in ratings_by_j:
      accum = 0
      for i, r in ratings_by_j[j]:
        accum += (r - U[i,:].dot(V[:,j]) - B[i] - mu)
      C[j] = accum / (1 + reg) / len(ratings_by_j[j])

  # update V
  for j in xrange(N):
    if j in ratings_by_j:
      matrix = np.zeros((K, K)) + reg*np.eye(K)
      vector = np.zeros(K)
      for i, r in ratings_by_j[j]:
        matrix += np.outer(U[i,:], U[i,:])
        vector += (r - B[i] - C[j] - mu)*U[i,:]
      V[:,j] = np.linalg.solve(matrix, vector)