Resharper 8.2的“安装”问题

概述

完美解决Resharper 8.2的“安装”问题和VS2012写Javascript语句无法智能提示的问题；

目录

引言——Resharper 简介——安装——VS2012智能提示测试

---

引言

最近，在使用ArcGIS JS API搞开发，按照ArcGIS JS API官网提供的开发环境设置帮助，详情可参考这里，我的IDE选用VS2012,并下载好了本地的“jsapi_vsdoc12_v33.js”文件，下载地址，点这里，

在单独的js文件中写代码，vs2012总是无法智能提示，很纠结！在谷歌中来回了N次，在VS中实验了N次，发现有三种办法可解决VS2012无法智能提示（intellisense）的问题，分别是：

1. 安装Resharper
2. 将jsapi_vsdoc12_v33.js文件复制到VS2012的javascript的Web引用目录
3. 传统方法，添加_reference.js，在单独的js文件中，引用/// <reference path="path_to_the_code_assist_document" />

本文只讨论第一种方法，其他二种方法请移步我的另外一篇博客，点这里。

Resharper 简介

ReSharper是一个JetBrains公司出品的著名的代码生成工具，其能帮助Microsoft Visual Studio成为一个更佳的IDE。它包括一系列丰富的能大大增加C#和Visual Basic .net开发者生产力的特征。使用ReSharper，你可以进行深度代码分析，智能代码协助，实时错误代码高亮显示，解决方案范围内代码分析，快速代码 更正，一步完成代码格式化和清理，业界领先的自动代码重构，高级的集成单元测试方案，和强大的解决方案内导航和搜索。

详情请见：http://baike.baidu.com/link?url=AImNJbjZQ8Hfhps3OTcJldRfw2gl3OlJ2POQ5diJqgteEfPZRiWS6snI9b2HUFDchSFDGaRaoGIOmaeuwQAulK

安装

1.下载安装文件Reshaper8.2安装包和crack文件，点这里；

2.正常步骤安装Reshaper8.2；

3.启动VS2012，默认会打开Resharper的License Information窗口；

4.获取user name和license key；

1）打开kegen程序，如下图：

2）输入用户名，例如：yc，单击Enter键，如下图：

 

 

5.输入user name和license key；坑爹啊，发现dos窗体不提供复制的功能，手工输入！完成如下，见下图：

 

如若大家 习惯yc这个用户名，可以用下面的用户名和key激活，免得手动输入一个这么不规则的license key！

user name: yc     

license key: aX0wfMXA3Mgy1+WoDZLuEZL28YGV65ta

 

单击OK，注册完成！选择使用shortcut keys的策略，完成！

 

 

 

VS2012智能提示测试

测试Resharper的智能提示；最后，测试下Resharper对于VS智能提示的改良，新建一个js文件，输入"es"，发现vs12能够完美提示，如下图：

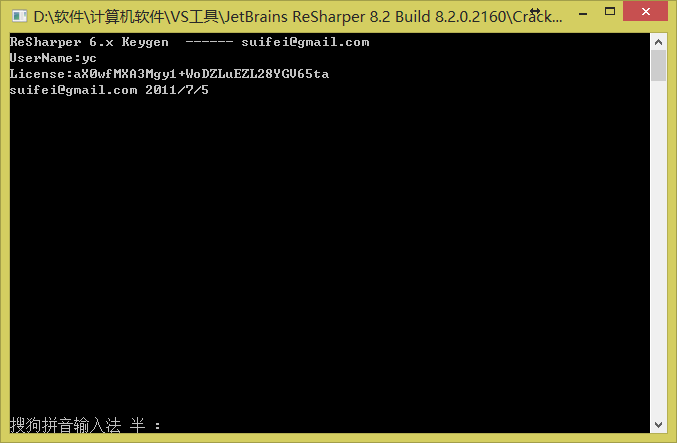
原创笔记，转载请注明出处！http://www.cnblogs.com/ArcScofield/

邮箱：ychaowhu@gmail.com