「LuoguP1341」 无序字母对（欧拉回路

题目描述

给定n个各不相同的无序字母对（区分大小写，无序即字母对中的两个字母可以位置颠倒）。请构造一个有n+1个字母的字符串使得每个字母对都在这个字符串中出现。

输入输出格式

输入格式：

第一行输入一个正整数n。

以下n行每行两个字母，表示这两个字母需要相邻。

输出格式：

输出满足要求的字符串。

如果没有满足要求的字符串，请输出“No Solution”。

如果有多种方案，请输出前面的字母的ASCII编码尽可能小的（字典序最小）的方案

输入输出样例

输入样例#1：
复制

4
aZ
tZ
Xt
aX

输出样例#1： 复制

XaZtX
 

说明

【数据规模与约定】

不同的无序字母对个数有限，n的规模可以通过计算得到。

---

题解

首先翻译一下题面吧。

给定n条无向边，试构造一条路径恰好经过每条边１次。

如果可以构造，输出途径的点的编号。

否则输出No Solution。

其实想明白所谓的字母对只是无向边的话，这道题就是很清晰的欧拉路径了。

——以下来自欧拉回路路径求解 - STILLxjy - CSDN博客——

Hierholzer 算法：
另一种计算欧拉路的算法是 Hierholzer 算法。这种算法是基于这样的观察：

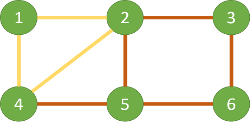
在手动寻找欧拉路的时候，我们从点 4 开始，一笔划到达了点 5，形成路径 4-5-2-3-6-5。此时我们把这条路径去掉，则剩下三条边，2-4-1-2 可以一笔画出。

这两条路径在点 2 有交接处（其实点 4 也是一样的）。那么我们可以在一笔画出红色轨迹到达点 2 的时候，一笔画出黄色轨迹，再回到点 2，把剩下的红色轨迹画完。

由于明显的出栈入栈过程，这个算法可以用 DFS 来描述。
如果想看得更仔细一点，下面是从点 4 开始到点 5 结束的 DFS 过程，其中 + 代表入栈，- 代表出栈。
4+ 5+ 2+ 3+ 6+ 5+ 5- 6- 3- 1+ 4+ 2+ 2- 4- 1- 2- 5- 4-
我们把所有出栈的记录连接起来，得到
5-6-3-2-4-1-2-5-4

诸位看官可以自己再选一条路径尝试一下。不过需要注意的是，起始点的选择和 Fleury 要求的一样。
这个算法明显要比 Fleury 高效，它不用判断每条边是否是一个桥。

Hierholzer的复杂度是$O(E)$的，所以就套欧拉路径的板子就好啦。

（实在没懂怎么“计算得到”n的规模，好在不用这个条件QAQ

 /*
     qwerta
     P1341 无序字母对
     Accepted
     100
     代码 C++，1.46KB
     提交时间 2018-09-30 11:11:47
     耗时/内存
     28ms, 1052KB
 */
 #include<algorithm>
 #include<iostream>
 #include<cstdio>
 #include<stack>
 using namespace std;
 int g[][];
 int d[];//度数
 stack<int>st;//这个是记录栈，不是搜索栈！
 void dfs(int x)//dfs找点
 {
     for(int j='A';j<='z';++j)//这样循环就可以保持字典序最小啦
     if(g[x][j])
     {
         g[x][j]--;
         g[j][x]--;//反向边也要删
         dfs(j);//继续递归
     }
     st.push(x);//出栈的时候记录下来
     return;
 }
 int fa[];//用并查集维护是否有多个联通块
 int fifa(int x)
 {
     if(fa[x]==x)return x;
     return fa[x]=fifa(fa[x]);
 }
 int main()
 {
     //freopen("a.in","r",stdin);
     ios::sync_with_stdio(false);
     cin.tie(false),cout.tie(false);//关闭同步流（cin伴侣
     int n;
     cin>>n;
     for(int i='A';i<='z';++i)//初始化并查集
     fa[i]=i;
     for(int i=;i<=n;++i)
     {
         char x,y;
         cin>>x>>y;
         g[x][y]++;
         g[y][x]++;//临接矩阵存边
         d[x]++;
         d[y]++;//度数＋＋
         int u=fifa(x),v=fifa(y);
         if(u!=v)fa[u]=v;//维护并查集
     }
     //判定是否有解
     int num=;
     for(int i='A';i<='z';++i)
     if(d[i]%==)num++;
     if(num!=&&num!=){cout<<"No Solution";return ;}
     int tag=;
     for(int i='A';i<='z';++i)
     if(d[i])
     {
         if(!tag)tag=i;
         else if(fifa(tag)!=fifa(i)){cout<<"No Solution";return ;}
     }
     //找是否有奇点
     int s=-;
     for(int i='A';i<='z';++i)
     if(d[i]%==){s=i;break;}
     if(s==-)//如果没有奇点就找AscII最小的点
       for(int i='A';i<='z';++i)
       if(d[i]){s=i;break;}
     dfs(s);//递归找点
     while(!st.empty())
     {
         cout<<(char)st.top();
         st.pop();
     }//输出
     return ;
 }

皮一下：