Codeforces Round #461 (Div. 2) B C D

题目链接：http://codeforces.com/contest/922

B. Magic Forest

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Imp is in a magic forest, where xorangles grow (wut?)

A xorangle of order n is such a non-degenerate triangle, that lengths of its sides are integers not exceeding n, and the xor-sum of the lengths is equal to zero. Imp has to count the number of distinct xorangles of order n to get out of the forest.

Formally, for a given integer n you have to find the number of such triples (a, b, c), that:

• 1 ≤ a ≤ b ≤ c ≤ n;
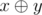• , where  denotes the bitwise xor of integers x and y.
• (a, b, c) form a non-degenerate (with strictly positive area) triangle.

Input

The only line contains a single integer n (1 ≤ n ≤ 2500).

Output

Print the number of xorangles of order n.

Examples

input

Copy

6

output

1

input

Copy

10

output

2

Note

The only xorangle in the first sample is (3, 5, 6).

题意：

求有多少对(a,b,c)满足：1 ≤ a ≤ b ≤ c ≤ n，且a^b^c = 0，且a、b、c满足三角形的条件。

题解：

1.虽然此题简单，但太久没打过比赛，所以还需要一定的反应时间。

2.一看到题目时，第一想法就是把n写成二进制形式，然后再用类似数位DP的方法统计。但是，这种想法想想就好了。

3.正确做法是枚举 a、b，且要求：a<=b，显然 c = a^b。此时，只需判断c是否满足： b ≤ c ≤ n 且 c<=(a+b-1)即可。

4.时间复杂度：O（n^2）。

代码如下：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <cmath>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 using namespace std;
 typedef long long LL;
 const int INF = 2e9;
 const LL LNF = 9e18;
 const int MOD = 1e9+;
 const int MAXN = 1e6+;

 int main()
 {
     int n;
     while(scanf("%d",&n)!=EOF)
     {
         LL ans = ;
         for(int i = ; i<=n; i++)   //枚举a
         for(int j = i; j<=n; j++)   //枚举b
             if( j<=(i^j) && (i^j)<=min(n,i+j-)) //则c = (a^b)，且 b<=c<=a+b-1,满足三角形，且还需c<=n
                 ans++;
         printf("%lld\n",ans);
     }
 }

C. Cave Painting

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Imp is watching a documentary about cave painting.

Some numbers, carved in chaotic order, immediately attracted his attention. Imp rapidly proposed a guess that they are the remainders of division of a number n by all integers i from 1 to k. Unfortunately, there are too many integers to analyze for Imp.

Imp wants you to check whether all these remainders are distinct. Formally, he wants to check, if all 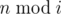, 1 ≤ i ≤ k, are distinct, i. e. there is no such pair (i, j) that:

• 1 ≤ i < j ≤ k,
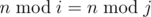• , where  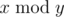is the remainder of division x by y.

Input

The only line contains two integers n, k (1 ≤ n, k ≤ 1018).

Output

Print "Yes", if all the remainders are distinct, and "No" otherwise.

You can print each letter in arbitrary case (lower or upper).

Examples

input

Copy

4 4

output

No

input

Copy

5 3

output

Yes

Note

In the first sample remainders modulo 1 and 4 coincide.

题意：

给出n、k，问是否满足所有n%i都唯一，其中 1<=i<=k。

题解：

1.此题自己没有想出来，看题解的。

2.可知：n%1 = 0，如要所有n%i都唯一，那么n%2是能为1，这也使得n%3只能为2，一直推下去，n%i = i-1。

3.根据第二点，只需枚举i，1<=i<=k，看是否存在i不满足n%i == i-1 即可。

4.关于时间复杂度：由于k<=1e18，所以即使是O(n)的时间复杂度也接受不了。但其实能使得n%i == i-1，1<=i<=k 的n、k范围应该都很小，只能说“应该”，证明就不会了。

代码如下：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <cmath>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 using namespace std;
 typedef long long LL;
 const int INF = 2e9;
 const LL LNF = 9e18;
 const int MOD = 1e9+;
 const int MAXN = 1e5+;

 int main()
 {
     LL n, k;
     while(scanf("%lld%lld", &n,&k)!=EOF)
     {
         bool flag = true;
         for(int i = ; i<=k; i++)
         {
             if(n%i!=i-)
             {
                 flag = false;
                 break;
             }
         }
         if(flag) puts("Yes");
         else puts("No");
     }
 }

D. Robot Vacuum Cleaner

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Pushok the dog has been chasing Imp for a few hours already.

Fortunately, Imp knows that Pushok is afraid of a robot vacuum cleaner.

While moving, the robot generates a string t consisting of letters 's' and 'h', that produces a lot of noise. We define noise of string t as the number of occurrences of string "sh" as a subsequence in it, in other words, the number of such pairs (i, j), that i < j 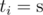and  and .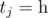

The robot is off at the moment. Imp knows that it has a sequence of strings ti in its memory, and he can arbitrary change their order. When the robot is started, it generates the string t as a concatenation of these strings in the given order. The noise of the resulting string equals the noise of this concatenation.

Help Imp to find the maximum noise he can achieve by changing the order of the strings.

Input

The first line contains a single integer n (1 ≤ n ≤ 105) — the number of strings in robot's memory.

Next n lines contain the strings t1, t2, ..., tn, one per line. It is guaranteed that the strings are non-empty, contain only English letters 's' and 'h' and their total length does not exceed 105.

Output

Print a single integer — the maxumum possible noise Imp can achieve by changing the order of the strings.

Examples

input

Copy

4
ssh
hs
s
hhhs

output

18

input

Copy

2
h
s

output

1

Note

The optimal concatenation in the first sample is ssshhshhhs.

题意：

给出n个“sh”串，问怎样把他们拼接在一起，使得凭借后新串的(s,h)对最多？

题解：

1.拿到题目的第一感觉是：对于一个串来说，如果s所占的比例越大，那么它就应该越靠前。

2.如果两个串s所占的比例一样，经过比划了一下，长度较长的那个应该放在前面。

3.得出比较规则之后，就对这n个串进行排序，然后统计即可。

4.对于上述方法，也没有去证明它的正确性，凭感觉大概就这样。

代码如下：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <cmath>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 using namespace std;
 typedef long long LL;
 const int INF = 2e9;
 const LL LNF = 9e18;
 const int MOD = 1e9+;
 const int MAXN = 1e5+;

 struct node
 {
     string s;
     double p;
     bool operator<(const node &x)const{
         if(p==x.p) return s.size()>x.s.size();
         else return p>x.p;
     }
 }a[MAXN];

 int main()
 {
     int n;
     while(scanf("%d",&n)!=EOF)
     {
         for(int i = ; i<=n; i++)
         {
             cin>>a[i].s;
             int len = a[i].s.size(), cnt = ;
             for(int j = ; j<len; j++)
                 cnt += (a[i].s[j]=='s');
             a[i].p = 1.0*cnt/len;
         }

         sort(a+,a++n);
         LL ans = , cnt = ;
         for(int i = ; i<=n; i++)
         {
             int len = a[i].s.size();
             for(int j = ; j<len; j++)
             {
                 if(a[i].s[j]=='s') cnt++;
                 else ans += cnt;
             }
         }
         printf("%lld\n", ans);
     }
 }