洛谷 P3372 【模板】线段树 1

P3372 【模板】线段树 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数加上x

2.求出某区间每一个数的和

输入输出格式

输入格式：

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数加上k

操作2： 格式：2 x y 含义：输出区间[x,y]内每个数的和

输出格式：

输出包含若干行整数，即为所有操作2的结果。

输入输出样例

输入样例#1：

5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

输出样例#1：

11
8
20

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^，保证在int64/long long数据范围内）

样例说明：

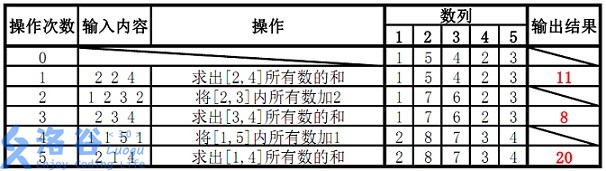
/*感觉好久没写线段树了，这是一个只牵扯到区间修改和区间查询的线段树模板，需要用懒标记,别忘开longlong*/
#include<iostream>
#include<cstdio>
using namespace std;
#define ll long long
ll n,m,opx,opy,opv,ans;
struct node{
    ll lazy,v,l,r;
}tr[*];
void build(int l,int r,int k){
    tr[k].l=l;tr[k].r=r;
    if(tr[k].l==tr[k].r){
        scanf("%lld",&tr[k].v);
        return;
    }
    int mid=(l+r)/;
    build(l,mid,k*);
    build(mid+,r,k*+);
    tr[k].v=tr[k*].v+tr[k*+].v;
}
void down(int k){
    ll v=tr[k].lazy;
    tr[k*].v+=v*(tr[k*].r-tr[k*].l+);
    tr[k*].lazy+=v;
    tr[k*+].v+=v*(tr[k*+].r-tr[k*+].l+);
    tr[k*+].lazy+=v;
    tr[k].lazy=;
}
void add(int k){
    if(tr[k].l>=opx&&tr[k].r<=opy){
        tr[k].v+=opv*(tr[k].r-tr[k].l+);
        tr[k].lazy+=opv;
        return;
    }
    if(tr[k].lazy)down(k);
    ll m=(tr[k].l+tr[k].r)/;
    if(opx<=m)add(k*);
    if(opy>m)add(k*+);
    tr[k].v=tr[k*].v+tr[k*+].v;
}
void ask(int k){
    if(tr[k].l>=opx&&tr[k].r<=opy){
        ans+=tr[k].v;
        return;
    }
    if(tr[k].lazy)down(k);
    int m=(tr[k].l+tr[k].r)/;
    if(opx<=m)ask(k*);
    if(opy>m)ask(k*+);
}
int main(){
    scanf("%lld%lld",&n,&m);
    build(,n,);int x;
    for(ll i=;i<=m;i++){
        scanf("%d",&x);
        if(x==){
            scanf("%d%d%lld",&opx,&opy,&opv);
            add();
        }
        if(x==){
            ans=;
            scanf("%d%d",&opx,&opy);
            ask();
            printf("%lld\n",ans);
        }
    }
}