javascript/js实现 排序二叉树数据结构 学习随笔

二叉树是一种数据结构。其特点是：

1.由一系列节点组成，具有层级结构。每个节点的特性包含有节点值、关系指针。节点之间存在对应关系。

2.树中存在一个没有父节点的节点，叫做根节点。树的末尾存在一系列没有子节点的节点，称为叶子节点。其他可以叫做中间节点。

3.树的根节点位于第一层，层级数越大，节点位置越深，层级数也叫做树高。

排序二叉树为二叉树的一种类型，其特点是：

1.节点分为左右子树。

2.在不为空的情况下，左子树子节点的值都小于父节点的值。

3.在不为空的情况下，右子树子节点的值都大于父节点的值。

4.每个节点的左右子树都按照上述规则排序。

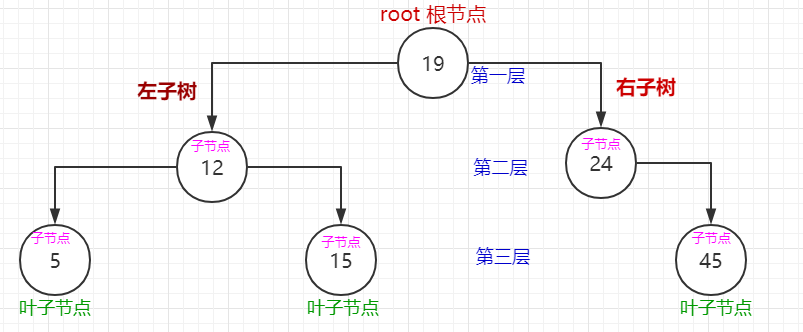
如图：

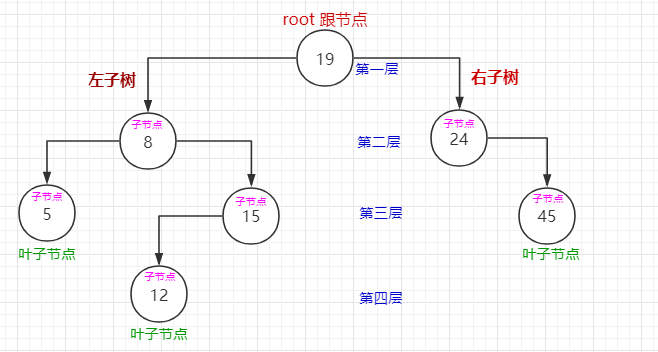（打错字了..）

js代码来实现上述数据结构：

1.节点用对象来描述，节点特性用对象属性来描述。

 class Node {
   constructor(key) {
     this.key = key;// 节点值
     this.left = null;// 左指针
     this.right = null;// 右指针
   }
 }

2.二叉树结构用对象来描述。

 // 二叉树
 class BinaryTree {
   constructor() {
     this.root = null;// 根节点
   }
   insert(key) {// api--插入
     const newNode = new Node(key);
     if (this.root === null) {// 设置根节点
       this.root = newNode;
     }
     method.insertNode(this.root, newNode);
   }
 }

相关方法：

 // method
 method = {
   insertNode(root, newNode) {
     if (newNode.key < root.key) {// 进入左子树
       if (root.left === null) {// 左子树为空
         root.left = newNode;
       } else {// 左子树已存在
         method.insertNode(root.left, newNode);
       }
     } else if (newNode.key > root.key) {// 进入右子树
       if (root.right === null) {// 右子树为空
         root.right = newNode;
       } else {// 右子树已存在
         method.insertNode(root.right, newNode);
       }
     }
   }
 };

具体用法：

 // 实例化二叉树
 const binaryTree = new BinaryTree();
 
 // key值
 const keys = [, , , , , , ];
 
 // 生成排序二叉树
 keys.forEach(key => binaryTree.insert(key));

结果：

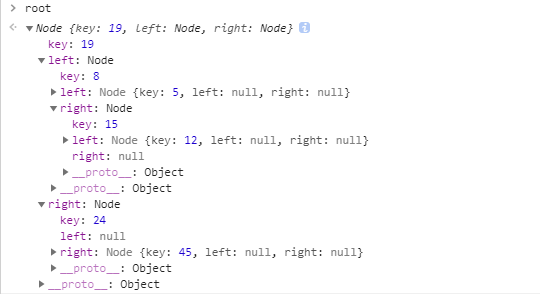
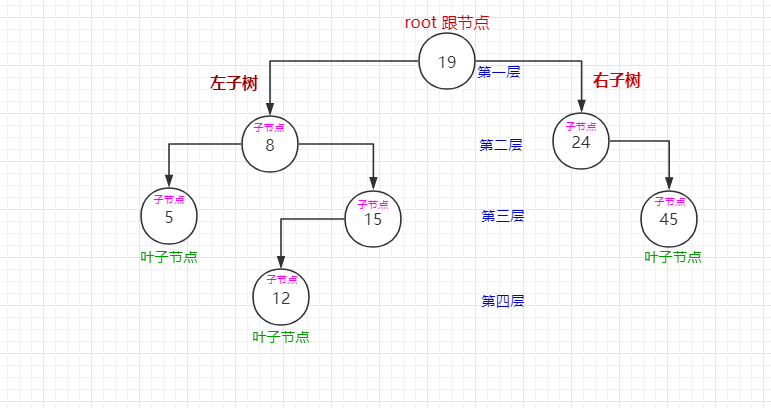
排序二叉树的遍历：

一、中序遍历

（1）以上图为例，中序遍历顺序为： 5 - 8 - 12 - 15 - 19 - 24 - 45。

（2）总是先遍历左子树，然后访问根节点，接着遍历右子树。

代码实现：

 class BinaryTree {
   ...
   // callback为访问节点时执行的操作
   inorderTraversal(callback) {// api--中序遍历
     method.inorderTraversalNode(this.root, callback);
   }
 }
 
 method = {
   ...
 
   inorderTraversalNode(node, callback) {
     if (node) {// 当前节点
       method.inorderTraversalNode(node.left, callback);// 遍历左子树
       callback(node);// 访问节点
       method.inorderTraversalNode(node.right, callback);// 遍历右子树
     }
   },
 };
 
 // 中序遍历
 binaryTree.inorderTraversal(node => console.log(node.key));

 // key值
 const keys = [19, 8, 15, 24, 45, 12, 5];

输入结果：5 - 8 - 12 - 15 - 19 - 24 - 45

二、前序遍历

（1）以上图为例，前序遍历顺序为： 19 - 8 - 5 - 15  - 12 - 24 - 45。

（2）总是先访问根节点，然后遍历左子树，接着遍历右子树。

代码实现：

 class BinaryTree {
   ...
   preOrderTraversal(callback) {// api--前序遍历
     method.preOrderTraversalNode(this.root, callback);
   }
 }
 
 method = {
   ...
   preOrderTraversalNode(node, callback) {
     if (node) {// 当前节点
       callback(node);// 访问节点
       method.preOrderTraversalNode(node.left, callback);// 遍历左子树
       method.preOrderTraversalNode(node.right, callback);// 遍历右子树
     }
   }
 };
 
 // 前序遍历
 binaryTree.preOrderTraversal(node => console.log(node.key));

 // key值
 const keys = [19, 8, 15, 24, 45, 12, 5];

输入结果：19 - 8 - 5 - 15  - 12 - 24 - 45

三、后序遍历

（1）以上图为例，后序遍历顺序为： 5 - 12 - 15 - 8  - 45 - 24 - 19。

（2）先遍历左子树，接着遍历右子树，最后访问根节点。

代码实现：

 class BinaryTree {
   ...
   postOrderTraversal(callback) {// api--后序遍历
     method.postOrderTraversalNode(this.root, callback);
   }
 }
 
 method = {
   ...
   postOrderTraversalNode(node, callback) {
     if (node) {// 当前节点
       method.postOrderTraversalNode(node.left, callback);// 遍历左子树
       method.postOrderTraversalNode(node.right, callback);// 遍历右子树
       callback(node);// 访问节点
     }
   }
 };
 
 // 后序遍历
 binaryTree.postOrderTraversal(node => console.log(node.key));

 // key值
 const keys = [19, 8, 15, 24, 45, 12, 5];

输入结果：5 - 12 - 15 - 8  - 45 - 24 - 19

排序二叉树的查找：

（1）查找最大值。根据排序二叉树的特点，右子树的值都大于父节点的值。只需要进入节点的右子树查找，当某个节点的右子树为空时，该节点就是最大值节点。

代码实现：

 class BinaryTree {
   ...
   max() {
     return method.maxNode(this.root);
   }
 }
 
 method = {
   ...
   maxNode(node) {
     if (node) {
       while(node.right !== null) {// 右子树不为空时
         node = node.right;
       }
       return node.key;
     }
     return null;
   }
 };

 // key值
 const keys = [19, 8, 15, 24, 45, 12, 5];

结果：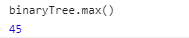

（2）查找最小值。根据排序二叉树的特点，左子树的值都小于父节点的值。只需要进入节点的左子树查找，当某个节点的左子树为空时，该节点就是最小值节点。

代码实现：

 1 class BinaryTree {
 2   ...
 3   min() {
 4     return method.minNode(this.root);
 5   }
 6 }
 7
 8 method = {
 9   ...
10   minNode(node) {
11     if (node) {
12       while(node.left!== null) {// 左子树不为空时
13         node = node.left;
14       }
15       return node.key;
16     }
17     return null;
18   }
19 };

 // key值
 const keys = [19, 8, 15, 24, 45, 12, 5];

结果：

（3）查找给定值。在排序二叉树中查找有没有节点对应的值与给定值相同。

根据排序二叉树的特点，比较给定值与节点值，小于时进入节点左子树。大于时进入节点右子树。等于时返回真。层层对比，最后如果子树为空，则表示没有找到。

代码实现：

 class BinaryTree {
   ...
   search(key) {
     return method.searchNode(this.root, key);
   }
 }
 
 method = {
   ...
   searchNode(node, key) {
     if (node === null) {// 没有找到
       return false;
     }
     if (key < node.key) {// 进入左子树
       return method.searchNode(node.left, key);
     } else if (key > node.key) {// 进入右子树
       return method.searchNode(node.right, key);
     } else {// 找到了
       return true;
     }
   }
 };

 // key值
 const keys = [19, 8, 15, 24, 45, 12, 5];

结果：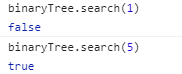

排序二叉树的删除：

当删除的节点为叶子节点时，直接把叶子节点设置成空。如图：删除值为5的节点。

原：

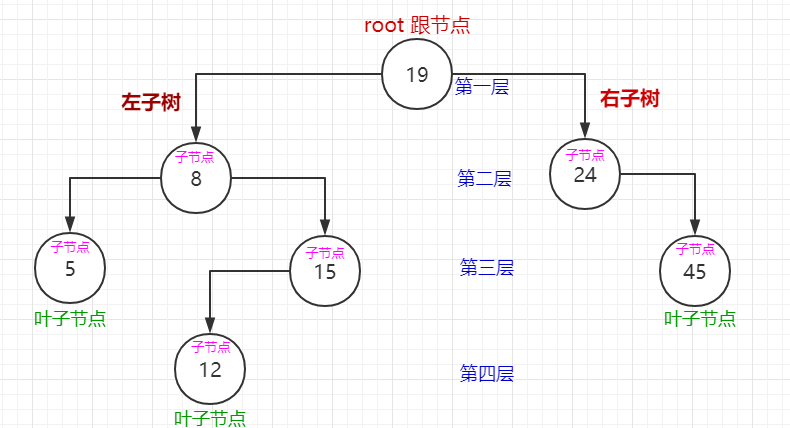
现：

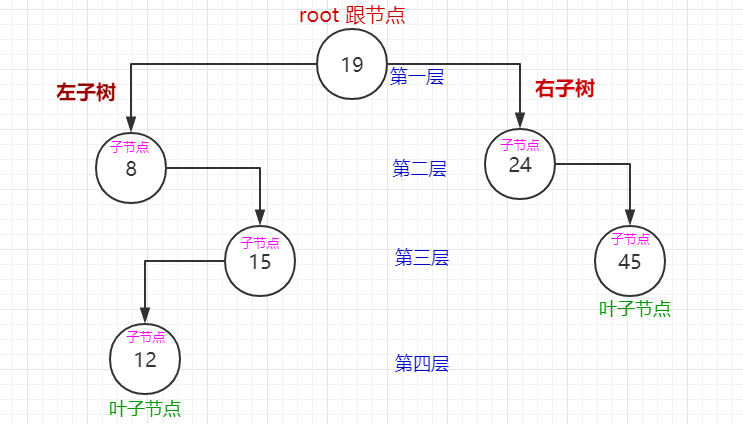
当删除的节点存在左子树时，把父节点的关系指针直接指向左子树。如图：删除值为15的节点。存在右子树时同理。

原：

现：

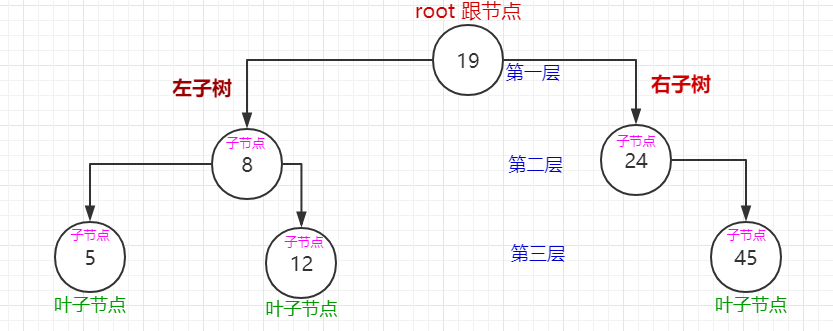
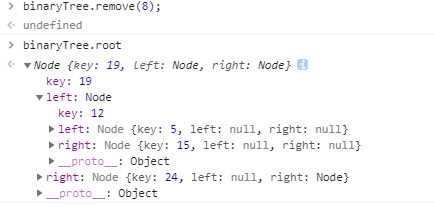
当节点存在左右子树时，先去右子树里找到最小值，然后用最小值替换节点值，最后进入右子树删除最小值对应的节点。如图：删除值为8的节点。

原：

现：

代码实现：

 class BinaryTree {
   ...
   remove(key) {
     this.root = method.removeNode(this.root, key);
   }
 }
 
 method = {
   ...
   removeNode(node, key) {
     if(node === null) {// 没有找到值对应的节点
       return null;
     }
     if (key < node.key) {// 给定值小于当前节点值
       node.left = method.removeNode(node.left, key);
       return node;
     } else if (key > node.key) {// 给定值大于当前节点值
       node.right = method.removeNode(node.right, key);
       return node;
     } else {// 找到给定值对应的节点
       if (node.left === null && node.right === null) {// 节点为叶子节点
         node = null;
         return node;
       }
 
       if (node.left === null) {// 节点存在右子树
         node = node.right;
         return node;
       } else if (node.right === null) {// 节点存在左子树
         node = node.left;
         return node;
       }
 
       // 节点存在左右子树时，先去右子树里找到最小值，然后用最小值替换节点值，最后进入右子树删除最小值对应的节点。
       const minKey = method.minNode(node.right);
       node.key = minKey;
       method.removeNode(node.right, minKey);
       return node;
     }
   }
 };

结果：

累死我了。。。