test20181102 空间复杂度 和 test20181030 数独

空间复杂度

考场做法

前有时间复杂度，后有空间复杂度。

但是这题不会有CE情况，所以较为好写。

就用map存复杂度，单层循环就搞定了。

至于判断维度的方法，我是用快读从字符串中读入。

然后不管常数，把所有的n都变成0，判断有几个0就好了。

using namespace std;

map<string,int>M;
char opt[MAXL];
char name[MAXL];
int maxcomp,curcomp;

int main()
{
	freopen("complexity.in","r",stdin);
	freopen("complexity.out","w",stdout);
	M["i"]=0;
	while(~scanf("%s",opt))
	{
		if(opt[0]=='S')
		{
			scanf("%s",name);
			maxcomp=0;
		}
		else if(opt[0]=='E')
		{
			M[name]=maxcomp;
//			cerr<<name<<" comp="<<maxcomp<<endl;
		}
		else
		{
			curcomp=M[opt];
//			cerr<<" "<<opt<<" comp="<<curcomp<<endl;
			fgets(buf,MAXL,stdin);
			len=strlen(buf);
			buf[--len]=0;
			p=0;
			for(int i=0;i<len;++i)
				if(buf[i]=='n')
					buf[i]='0';
			while(p<len)
			{
				int mul=read<int>();
//				cerr<<"  mul="<<mul<<endl;
				if(mul==0)
					++curcomp;
			}
			maxcomp=max(maxcomp,curcomp);
		}
	}
	int ans=0;
	for(map<string,int>::iterator i=M.begin();i!=M.end();++i)
		ans=max(ans,i->second);
	if(ans==0)
	{
		puts("O(1)");
	}
	else if(ans==1)
	{
		puts("O(n)");
	}
	else
	{
		printf("O(n^%d)\n",ans);
	}
	return 0;
}

标解

这东西是用markdown写的，底色挺好看，不知道怎么弄的。

#include <bits/stdc++.h>

#define For(i, l, r) for(register int i = (l), i##end = (int)(r); i <= i##end; ++i)

using namespace std;

template<typename T> inline bool chkmin(T &a, T b) {return b < a ? a = b, 1 : 0;}
template<typename T> inline bool chkmax(T &a, T b) {return b > a ? a = b, 1 : 0;}

inline int read() {
	int x(0), sgn(1); char ch(getchar());
	for (; !isdigit(ch); ch = getchar()) if (ch == '-') sgn = -1;
	for (; isdigit(ch); ch = getchar()) x = (x * 10) + (ch ^ 48);
	return x * sgn;
}

void File() {
	freopen ("complexity.in", "r", stdin);
	freopen ("complexity.out", "w", stdout);
}

map<string, int> M;
int ans = 0; string str;

int main () {

	File();

	M["i"] = 0;
	int ans = 0;

	while (cin >> str) {
		int maxv = 0;
		string name; cin >> name;
		while (cin >> str) {
			if (str[0] == 'E') break;
			int cur = M[str];
			cin >> str;
			For (j, 0, str.size() - 1)
				if (str[j] == 'n') ++ cur;
			chkmax(maxv, cur);
		}
		chkmax(ans, maxv);
		M[name] = maxv;
	}

	if (ans == 0) return puts("O(1)"), 0;
	if (ans == 1) return puts("O(n)"), 0;
	printf ("O(n^%d)\n", ans);

	return 0;

}

std直接找n有几个……我还是太年轻了。

数独

输入格式

输入的前 19 行为一个二维字符数组，为数独的初始状态的方阵格式。

随后一行一个整数 T 表示操作的次数。

随后 T 行，每行为下列形式：

• Insert x y k，表示在(x, y)位置插入数 k。
• Delete x y，表示删除(x, y)位置的数。
• Query x y，表示查询(x, y)位置能填入且不会出现冲突的数。
• Merge i j，表示合并第 i 次操作后的状态和第j 次操作后的状态。
• Print，表示查询整个数独的状态。

其中 x 表示行数，从上到下分别为 1 到 9，y 表示列数，从左到右分别为 1到 9。

输出格式

对于每个操作，你需要按照题目描述进行对应的输出。

样例输入输出 1

见题目目录下的 1.in 与 1.ans。

样例输入输出 2

见题目目录下的 2.in 与 2.ans。

该样例的数据规模与第 6 / 7 个测试点相同。

数据规模与约定

所有测试点的数据规模与约定如下：

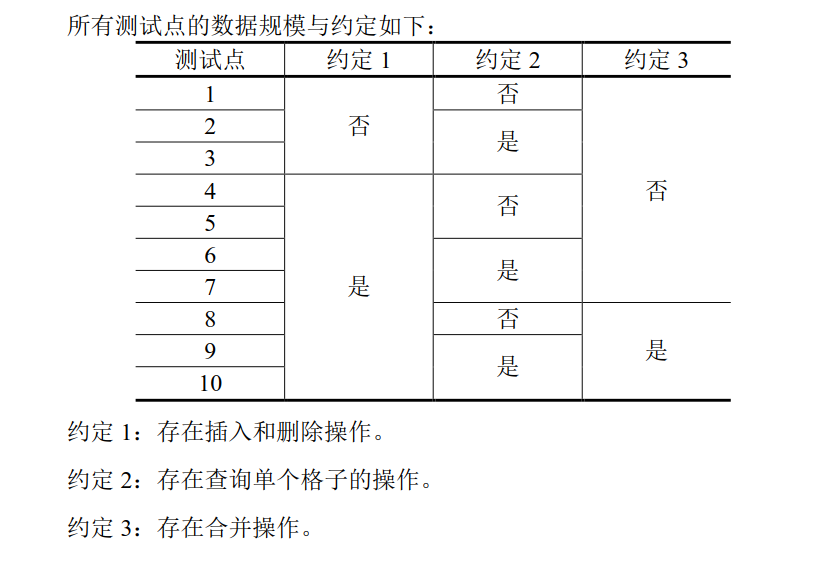
对于所有的数据，\(1 \leq T \leq 100，1 \leq x, y,k \leq 9\)，对于第 a 个操作，若是Merge操作，则\(1 \leq i, j <a\)。保证第一个操作不是 Merge操作。

对于所有的数据，均可能存在查询整个数独的操作，且保证初始状态不存在冲突。

分析

照题目模拟即可。

下标从0开始判同九宫格会很好写。

封装check函数会让代码简洁很多。

#include<iostream>
#include<cstdio>
#include<cstring>
template<class T>T read(T&x)
{
	T data=0;
	char ch=getchar();
	while(!isdigit(ch))
	{
		ch=getchar();
	}
	while(isdigit(ch))
	{
		data=data*10+ch-'0';
		ch=getchar();
	}
	return x=data;
}
using namespace std;

const int MAXN=150;
int n,a[20];
struct Soduku
{
	int data[9][9];

	void init()
	{
		memset(data,0,sizeof data);
	}

	Soduku()
	{
		init();
	}

	int*operator[](const int&x)
	{
		return data[x];
	}

	int chk(int x,int y,int k) // x-1,y-1
	{
		if(data[x][y]) // err
		{
			return 1;
		}
		for(int i=0;i<9;++i)
			if(data[x][i]==k) // row
			{
				return 2;
			}
		for(int i=0;i<9;++i)
			if(data[i][y]==k) // col
			{
				return 3;
			}
		int r=x/3,c=y/3;
		for(int i=r*3;i<(r+1)*3;++i)
			for(int j=c*3;j<(c+1)*3;++j)
				if(data[i][j]==k)
				{
					return 4; // squ
				}
		return 0; // ok
	}

	void ins(int x,int y,int k) // x-1,y-1
	{
		int stat=chk(x,y,k);
		if(stat==1)
		{
			puts("Error!");
			return;
		}
		else if(stat==2)
		{
			puts("Error:row!");
			return;
		}
		else if(stat==3)
		{
			puts("Error:column!");
			return;
		}
		else if(stat==4)
		{
			puts("Error:square!");
			return;
		}
		else
		{
			puts("OK!");
			data[x][y]=k;
		}
	}

	void del(int x,int y) // x-1,y-1
	{
		if(!data[x][y])
		{
			puts("Error!");
			return;
		}
		puts("OK!");
		data[x][y]=0;
	}

	void quiz(int x,int y) // x-1,y-1
	{
		if(data[x][y])
		{
			puts("Error!");
			return;
		}
		n=0;
		for(int k=1;k<=9;++k) // try i
		{
			if(chk(x,y,k)==0)
				a[++n]=k;
		}
		printf("%d\n",n);
		for(int i=1;i<=n;++i)
			printf("%d\n",a[i]);
	}

	Soduku operator+(const Soduku&rhs)const
	{
		Soduku res;
		int icnt=0,jcnt=0; // edit 1
		for(int i=0;i<9;++i)
			for(int j=0;j<9;++j)
			{
				if(data[i][j]&&res.chk(i,j,data[i][j])==0)
				{
					res.data[i][j]=data[i][j];
					++icnt;
					continue;
				}
				if(rhs.data[i][j]&&res.chk(i,j,rhs.data[i][j])==0)
				{
					res.data[i][j]=rhs.data[i][j];
					++jcnt;
					continue;
				}
			}
		printf("%d %d\n",icnt,jcnt);
		return res; // eidt 2
	}

	void out()
	{
		for(int i=0;i<9;++i)
		{
			puts("+-+-+-+-+-+-+-+-+-+");
			for(int j=0;j<9;++j)
				printf("|%d",data[i][j]);
			printf("|\n");
		}
		puts("+-+-+-+-+-+-+-+-+-+");
	}
}S[MAXN];

int main()
{
	freopen("sudoku.in","r",stdin);
	freopen("sudoku.out","w",stdout);
	for(int i=0;i<9;++i)
		for(int j=0;j<9;++j)
			read(S[0][i][j]);
	int T;
	read(T);
//	cerr<<"T="<<T<<endl;
	char opt[20];
	int x,y,k;
	for(int i=1;i<=T;++i)
	{
		S[i]=S[i-1];
		scanf("%s",opt);
		if(opt[0]=='I') // Insert x y k
		{
			read(x);read(y);read(k);
			--x,--y;
			S[i].ins(x,y,k);
		}
		else if(opt[0]=='D') // Delete x y
		{
			read(x);read(y);
			--x,--y;
			S[i].del(x,y);
		}
		else if(opt[0]=='Q') // Query x y
		{
			read(x);read(y);
			--x,--y;
			S[i].quiz(x,y);
		}
		else if(opt[0]=='M') // Merge i j
		{
			read(x);read(y);
			S[i]=S[x]+S[y];
		}
		else if(opt[0]=='P') // Print
		{
			S[i].out();
		}
//		cerr<<i<<" S="<<endl;
//		S[i].out();
	}
	return 0;
}