二叉树实例学习（四）——获取节点的高度函数getHight()

树T中所有节点深度的最大值称为该树的高度（height），实际上每个节点与其所有子节点都可以看做一颗树，也就是说除了根结点，所有子结点都可以看做是一颗子树，因此每个结点都有树高。在本程序中约定，仅含单个结点的树高为0，空树高度为-1。据此，编写getHight()：

    int getHight(BinNodePosi(T) x)
    {
        int l_hight,r_hight;
        if(x==NULL)
            return -;
        else if(!hasChild(*x))
        {
            return ;
        }
        else
        {
            l_hight = getHight(x->lc)+;
            r_hight = getHight(x->rc)+;
        }
        return l_hight>r_hight?l_hight:r_hight;
    }

结点类定义代码如下：

#ifndef BINNODE
#define BINNODE
#include <iostream>
//***************************************************************************************
///代码5.2 ， BinNode状态与性质的判断
///一、 判断该节点是什么！
/// 是否是根节点、是否是左子节点、是否是右子节点、是否是叶节点
#define isRoot(x) (!((x).parent))
#define isLChild(x) (!isRoot(x)&&(&(x)==(x).parent->lc))  //不是根节点，同时必须是父节点的左孩子
#define isRChild(x) (!isRoot(x)&&(&(x)==(x).parent->rc))  //不是根节点，同时必须是父节点的右孩子
///二、判断该节点有什么
//判断是否有孩子
#define hasLChild(x) ((x).lc!=NULL)  //判断节点x是否有左孩子
#define hasRChild(x) ( (x).rc )      //判断节点x 是否有右孩子
#define hasChild(x)  ( hasLChild(x)||hasRChild(x))  //判断节点x是否有孩子（左、右至少有一个）
//判断是否为叶节点
#define isLeaf(x)   ( !hasChild(x) )   //判断节点x是否是叶子节点

//****************************************************************************************
#define BinNodePosi(T) BinNode<T>* //节点位置

typedef enum{RB_RED,RB_BLACK} RBColor;//节点颜色

template <typename T>
class BinNode
{
public:
    T data;//数值
    int height;
    int npl;//Null Path Length(左式堆，也可直接用height代替)
    RBColor color;
    BinNodePosi(T) parent;//父节点
    BinNodePosi(T) lc;//左子节点
    BinNodePosi(T) rc;//右子节点
    //构造函数
    BinNode():parent(NULL),lc(NULL),rc(NULL),height(),npl(),color(RB_RED){}
    BinNode(T e,BinNodePosi(T) p=NULL,BinNodePosi(T) lc=NULL,BinNodePosi(T) rc=NULL,
            int h=,int l=,RBColor c=RB_RED)
    {
        data=e;
        parent=p;
        this->lc=lc,this->rc=rc;//此处添加this指针，以便将成员变量lc、rc与形参lc和rc区分

        height=h;
        npl=l;
        color=c;
    }
///***********插入孩子节点*******************************
/// 将数据e作为当前节点的左孩子或右孩子插入，并返回该节点指针
    BinNodePosi(T) insertAsLC(T const&e)
    {
        return lc=new BinNode(e,this);
    }
    BinNodePosi(T) insertAsRC(T const&e)
    {
        return rc=new BinNode(e,this);
    }
};
#endif // BINNODE

树的定义代码如下：

#ifndef BINTREE
#define BINTREE
#include<binnode.h>

template<typename T>
class BinTree
{
public:
    int _size;
    BinNodePosi(T) _root;//根结点指针
    int getHight(BinNodePosi(T) x)
    {
        int l_hight,r_hight;
        if(x==NULL)
            return -;
        else if(!hasChild(*x))
        {
            return ;
        }
        else
        {
            l_hight = getHight(x->lc)+;
            r_hight = getHight(x->rc)+;
        }
        return l_hight>r_hight?l_hight:r_hight;
    }

    virtual int updateHeight(BinNodePosi(T) x)//更新节点x的高度
    {

    }

//    void updateAboveHeight(BinNode<T> *x);//跟新节点x及其祖先的高度
public:
    BinTree():_size(),_root(NULL){}
    int size()const{return _size;}//获取树的规模，即共有多少个节点
    bool empty(){return !_root;}//判断是否为空树
    BinNodePosi(T) root()const{return _root;}//获取根结点指针
    BinNodePosi(T) insertAsRoot(T const&e)
    {
        _size=;
        return _root=new BinNode<T>(e);
    }

    BinNodePosi(T) insertAsLC(BinNodePosi(T) x,T const&e)
    {
        _size++;x->insertAsLC(e);
        x->height =getHight(x);
        return x->lc;
    }
    BinNodePosi(T) insertAsRC(BinNodePosi(T) x,T const&e)
    {
        _size++;x->insertAsRC(e);
        x->height=getHight(x);
        return x->rc;
    }
};

#endif // BINTREE

在测试程序中设计了六个结点的二叉树：

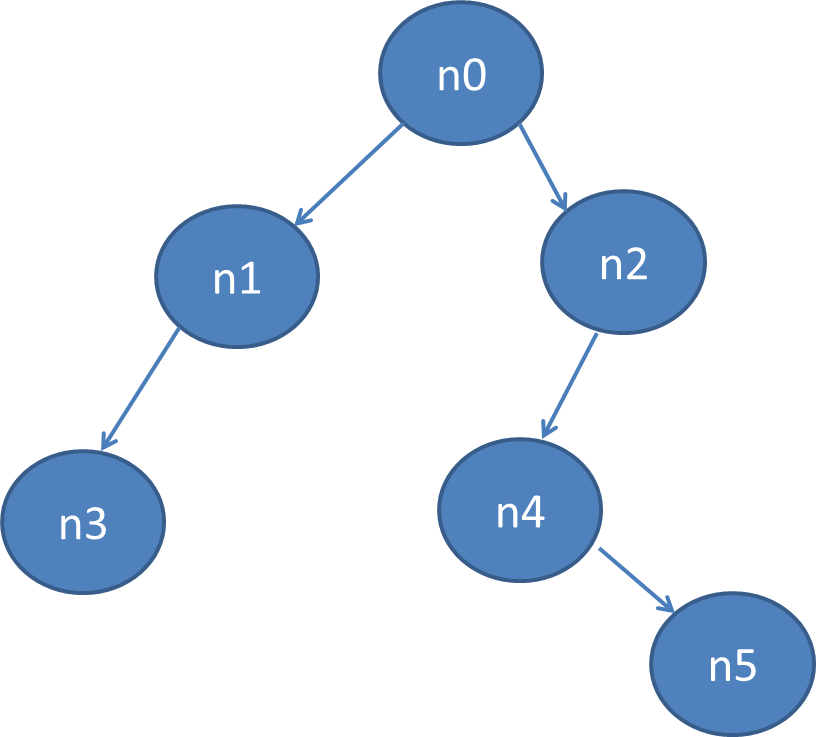
测试程序代码如下：

int main()
{
    BinNode<string>* n[];//数组指针

    BinTree<string> bt;
    n[]= bt.insertAsRoot("n0");
   n[]= bt.insertAsLC(n[],"n1");
   n[]= bt.insertAsRC(n[],"n2");
   n[]= bt.insertAsLC(n[],"n3");
   n[]=bt.insertAsLC(n[],"n4");
   n[]=bt.insertAsLC(n[],"n5");

    //测试根结点的高度
    cout<<bt.getHight(n[])<<endl;
    cout<<bt._root->height<<endl;

    return ;
}

运行结果如下：

由于每次插入新结点，都没有对插入结点的父辈结点更新高度，所以bt树的根结点的高度始终为1.