【转】GMM与K-means聚类效果实战

原地址：

GMM与K-means聚类效果实战

备注

分析软件：python

数据已经分享在百度云：客户年消费数据

密码：lehv

该份数据中包含客户id和客户6种商品的年消费额，共有440个样本

正文

一、数据探索和预处理

1.读取数据

import numpy as np
import pandas as pd

data = pd.read_excel(r'C:\Users\user\Desktop\客户年消费数据.xlsx')

2.缺失检查

print('各字段缺失情况：\n', data.isnull().sum())

输出：

id                  0
Fresh               0
Milk                0
Grocery             0
Frozen              0
Detergents_Paper    0
Delicatessen        0
dtype: int64

观察得出：数据不存在缺失，且数据类型都为整数数值型

3.不同商品消费额分布

为了避免分布图右偏严重，剔除了大于95%分位数的极端值

import matplotlib.pyplot as plt
import seaborn as sns
六种商品年消费额分布图

fig = plt.figure(figsize=(16, 9))

for i, col in enumerate(list(data.columns)[1:]):

plt.subplot(321+i)

q95 = np.percentile(data[col], 95)

sns.distplot(data[data[col] < q95][col])

plt.show()

输出：

从图中看出：商品年消费额基本符合大于0的正态分布

4.极值和异常值处理

features = data[['Fresh', 'Milk', 'Grocery', 'Frozen', 'Detergents_Paper', 'Delicatessen']]
# 剔除极值或异常值
ids = []
for i in list(features.columns):
    q1 = np.percentile(features[i], 25)
    q3 = np.percentile(features[i], 75)
    intervel = 1.6*(q3 - q1)/2
    low = q1 - intervel
    high = q3 + intervel
    ids.extend(list(features[(features[i] <= low) |
                             (features[i] >= high)].index))
ids = list(set(ids))
features = features.drop(ids)

二、无监督学习-降维和聚类分析

1.整体思路

数据中没有没有明显的目标变量，因此只能对客户的消费特征进行分析，也就是机器学习中所指的无监督方法。这里利用K-means和GMM（Gaussian Mixture Model）两种聚类算法，尝试对客户进行聚类分析，并对比两种算法的聚类结果差异。为了方便分析聚类效果，先用PCA算法降六个特征维度降低到两维。

2.聚类算法原理简述

K-means聚类

该算法利用数据点之间的欧式距离大小，将数据划分到不同的类别，欧式距离较短的点处于同一类。算法结果直接返回的是数据点所属的类别。

GMM

全称Gaussian Mixture Model，可以简单翻译为高斯混合模型，Gaussian指高斯分布（也就是正态分布）。该算法假设所有数据点来自多个参数不同的高斯分布，来自同一分布的数据点被划分为同一类。算法结果返回的是数据点属于不同类别的概率。

3.数据降至二维（PCA）

# 计算每一列的平均值
meandata = np.mean(features, axis=0)
# 均值归一化
features = features - meandata
# 求协方差矩阵
cov = np.cov(features.transpose())
# 求解特征值和特征向量
eigVals, eigVectors = np.linalg.eig(cov)
# 选择前两个特征向量
pca_mat = eigVectors[:, ：2]
pca_data = np.dot(features , pca_mat)
pca_data = pd.DataFrame(pca_data, columns=['pca1', 'pca2'])
两个主成分的散点图

plt.subplot(111)

plt.scatter(pca_data['pca1'], pca_data['pca2'])

plt.xlabel('pca_1')

plt.ylabel('pca_2')

plt.show()

输出：

图2.1 前两个主成分散点图

说明：图2.1中，横轴代表第一主成分，纵轴代表第二主成分

4.数据降维后信息保留百分比

print('前两个主成分包含的信息百分比：{:.2%}'.format(np.sum(eigVals[:2])/np.sum(eigVals)))

输出：

前两个主成分包含的信息百分比：92.39%

5.客户聚类

该步骤中，主要是对降维后的二维数据进行GMM和K-means聚类。聚类类别分别为2,3,4,5时，对比时两种算法下，点的的划分结果，并以散点图展现。

先定义make_ellipses函数，用于画出GMM算法中的高斯分布区域：

import matplotlib as mpl
定义make_ellipses函数，根据GMM算法输出的聚类类别，画出相应的高斯分布区域

def make_ellipses(gmm, ax, k):

for n in np.arange(k):

if gmm.covariance_type == 'full':

covariances = gmm.covariances_[n][:2, :2]

elif gmm.covariance_type == 'tied':

covariances = gmm.covariances_[:2, :2]

elif gmm.covariance_type == 'diag':

covariances = np.diag(gmm.covariances_[n][:2])

elif gmm.covariance_type == 'spherical':

covariances = np.eye(gmm.means_.shape[1]) * gmm.covariances_[n]

v, w = np.linalg.eigh(covariances)

u = w[0] / np.linalg.norm(w[0])

angle = np.arctan2(u[1], u[0])

angle = 180 * angle / np.pi  # convert to degrees

v = 2. * np.sqrt(2.) * np.sqrt(v)

ell = mpl.patches.Ellipse(gmm.means_[n, :2], v[0], v[1],

180 + angle)

ell.set_clip_box(ax.bbox)

ell.set_alpha(0.3)

ax.add_artist(ell)

再根据模型输出，画出聚类结果对比图：

from sklearn.cluster import KMeans
from sklearn.mixture import GaussianMixture
from sklearn.metrics import silhouette_score

score_kmean = []

score_gmm = []

random_state = 87

n_cluster = np.arange(2, 5)

for i, k in zip([0, 2, 4, 6], n_cluster):

# K-means聚类

kmeans = KMeans(n_clusters=k, random_state=random_state)

cluster1 = kmeans.fit_predict(pca_data)

score_kmean.append(silhouette_score(pca_data, cluster1))
# gmm聚类
gmm = GaussianMixture(n_components=k, covariance_type='full', random_state=random_state)
cluster2 = gmm.fit(pca_data).predict(pca_data)
score_gmm.append(silhouette_score(pca_data, cluster2))

# 聚类效果图
plt.subplot(421+i)
plt.scatter(pca_data['pca1'], pca_data['pca2'], c=cluster1, cmap=plt.cm.Paired)
if i == 6:
    plt.xlabel('K-means')
plt.subplot(421+i+1)
plt.scatter(pca_data['pca1'], pca_data['pca2'], c=cluster2, cmap=plt.cm.Paired)
make_ellipses(gmm, ax, k)
if i == 6:
    plt.xlabel('GMM')

plt.show()

输出：

图2.2 聚类效果对比

说明：聚类类别分别为2,3,4,5时，两种聚类算法结果对比（左边是K-means，右边是GMM）；点的颜色相同代表被聚为同一类；右图中的透明椭圆区域，代表GMM算法估计出的隐藏高斯分布区域。

三、聚类效果分析

如何评判聚类结果呢？这里引入轮廓分析（Silhouette analysis），轮廓分析主要统计轮廓得分，该指标计算聚类类别与相邻类别之间的总体距离大小，从而判断聚类有效程度。

# 聚类类别从2到11，统计两种聚类模型的silhouette_score，分别保存在列表score_kmean 和score_gmm
score_kmean = []
score_gmm = []
random_state = 87
n_cluster = np.arange(2, 12)
for k in n_cluster:
    # K-means聚类
    kmeans = KMeans(n_clusters=k, random_state=random_state)
    cluster1 = kmeans.fit_predict(pca_data)
    score_kmean.append(silhouette_score(pca_data, cluster1))
    # gmm聚类
    gmm = GaussianMixture(n_components=k, covariance_type='spherical', random_state=random_state)
    cluster2 = gmm.fit(pca_data).predict(pca_data)
    score_gmm.append(silhouette_score(pca_data, cluster2))
得分变化对比图

sil_score = pd.DataFrame({'k': np.arange(2, 12),

'score_kmean': score_kmean,

'score_gmm': score_gmm})
K-means和GMM得分对比

plt.figure(figsize=(10, 6))

plt.bar(sil_score['k']-0.15, sil_score['score_kmean'], width=0.3,

facecolor='blue', label='Kmeans_score')

plt.bar(sil_score['k']+0.15, sil_score['score_gmm'], width=0.3,

facecolor='green', label='GMM_score')

plt.xticks(np.arange(2, 12))

plt.legend(fontsize=16)

plt.ylabel('silhouette_score', fontsize=16)

plt.xlabel('k')

plt.show()

输出：

图3.1 K-means和GMM得分对比

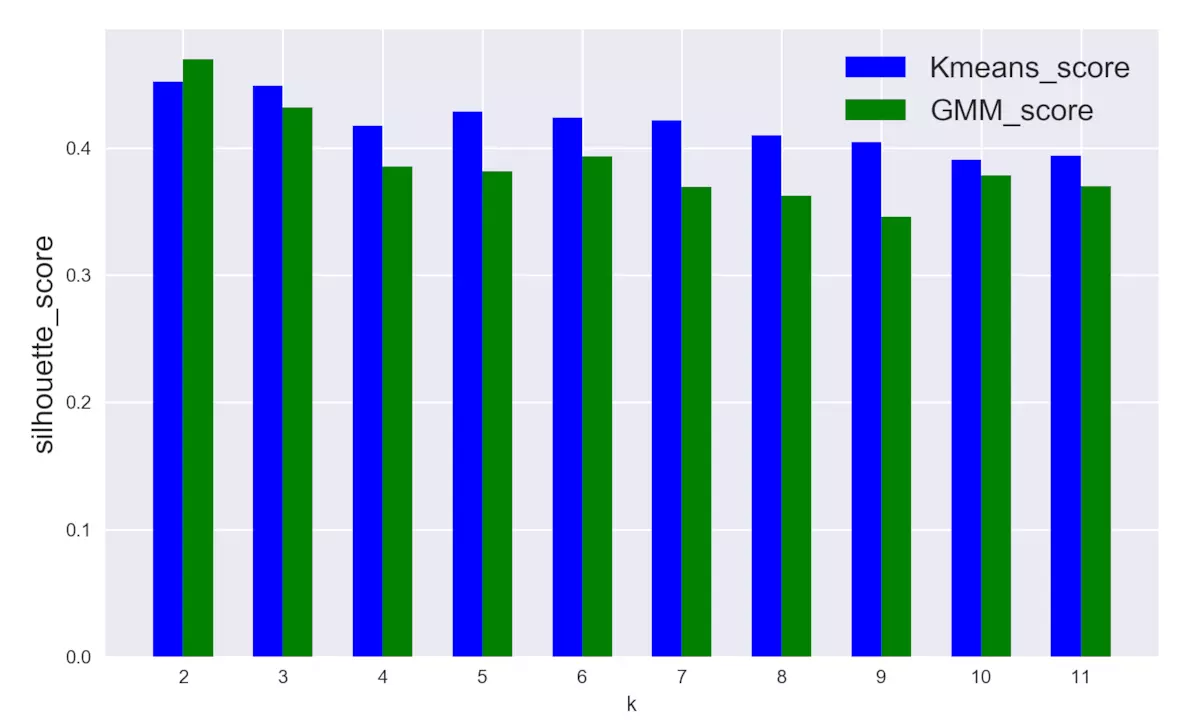
四、小结和建议

经过本次探索过程，总结以下几点：

1.图2.2，从点的划分情况来看，GMM和K-means的聚类结果具有较强的相似性；

2.图3.1， 从对比的角度，以silhouette_score为评判指标，整体上GMM的模型得分略低于K-means；

3.图3.1，聚类类别增多时，K-means模型的得分比较稳定，几乎没有明显差别，相比之下，GMM模型的得分开始下降幅度较大，但之后也趋于稳定。

4.根据得分情况，最佳聚类类别应该为2或3，此时K-means和GMM模型的表现都比较好。

5.最优k值对应的聚类类别可以作为新的数据特征，用于其它分析。

个人建议：若不考虑运算速度，当两种算法聚类得分差异很小时，推荐使用GMM算法，因为GMM能输出数据点属于某一类别的概率，因此输出的信息丰富程度大大高于K-means算法。

---

以上为转载内容。

在照葫芦画瓢的时候，遇到一点问题，主要是网络导致的python库文件下载速度慢和一点程序上的小问题。把两个下载时速度慢的库sklearn和xlrd放在github上了，整个python文件也在。

Github-GMM

sklearn.mixture.GaussianMixture 官方操作手册

从手册上查到

gmm.means_    //可以查看均值
gmm.covariances_    //可以查看均方差