”Unstanding the Bias-Variance Tradeoff“主题内容翻译

对预测模型讨论，预测误差（error）分两类：偏差（bias）造成的误差与方差（variance）造成的误差。最小化偏差与方差的一个权衡。理解这两类误差有利于诊断模型结果和避免过拟合和欠拟合。

偏差与方差

三种方式定义偏差与方差：概念、图形、数学

概念定义：

偏差造成的误差：预期/平均预测值和尝试正确预测的值之差。预期/平均预测值作何理解？多次建模，新数据新分析建立模型，由于数据随机，预测会产生一系列预测。偏见度量模型预测（models' predictions）远离正确值(the correct value)的程度.

方差造成的误差：对于给定数据点，模型预测的可变性。重复多次，方差就是对于给定点预测，在模型的不同实现之中变化的多少。

图形定义：

由靶心图可视化偏差与方差。靶心完全预测正确，偏离靶心预测差。训练中数据偶然变化。好的时候，集中在靶心；坏，outlier、非标准值（non-standard values）。散点图

图：

高/低偏差/方差

数学定义：

The Elements of Statistical Learning中的定义：

Variable:预测Y，协变量(covariate)X，存在一种关系，Y=f(X)+e，误差项e为零均值正态分布。

对f(X)估计一个模型f`(X)（利用线性回归或其他建模技术），故在一点x处的期望的预测误差的平方如下：Err(x)=E[(Y-f`(x))²].

误差可以分解为偏差项和方差项：

Err(x)=(E[f`(x)]-f(x))²+E[(f`(x)-E[f`(x)])²]+sigma_e²

Err(x)=Bias²+Variance+Irreducible Error

解释：第三项，束缚误差，噪音项，对于任何模型都无法从根本上降低。给真实模型和无限数据校准，应期盼使偏差项和方差项为0.但实际由于模型不完美及数据有限，采用一种减少偏差和最小化方差之间的权衡。

举例说明：投票

为下次选举投票共和党的人所占百分比建模。便于说明偏差和方差之间的差异。

50个电话，问卷调查投给谁，得到如下数据：

共和：13，民主：16，无回应：21 总：50

根据数据，投共和的概率：13/（13+16）=44.8%，民主会以高十个点赢得选举，但实际选举来临时，他们却以十个点输了。疑问：模型哪里有问题？

问卷的人不能代表所有人/没有跟进受访者，没有用加权等，样本量少。

把众多导致错误的原因归并到一个箱子中，它们实际上是造成偏差的不同来源，同时导致了方差。

电话采访/不与受访者跟进偏差来源、小样本方差来源。样本量增大，偏差依旧高，但方差减小。

用于训练模型的数据集提供先验，建模无法依靠增大数据量以减小方差。折中：偏差与方差，以减小总误差。

选民政党登记（属性信息）

选民属性：政党、财富、宗教

图，查看分布特性。坐标轴，财富、宗教

利用K近邻

查看某人最近的k个投票，利用距离测量，评估他的投票结果。

k近邻的关键：K的选取。

k=1，划分曲线参差不齐，k变大，过渡更平滑，岛块消失，k过大，分类区别模糊，边界线划分不能匹配。

k太小，岛块太多，方差太大。K太大，划分不准，高偏差。

此处k的选择可以看成是方差与偏差的一种权衡。

分析偏差和方差：

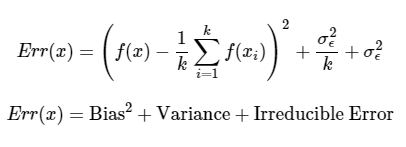
方差项为束缚误差的函数，k的方差误差随着k变大而下降。偏差项是函数粗糙到何种程度的模型空间。

处理偏差与方差

靠直觉

Bagging和重采样

　　随机森林

算法的渐近性质

　　渐进一致性、渐进效率。训练样本的规模趋于无穷时，偏差下降到0。

过拟合和欠拟合

　　处理偏差和方差实际上是处理过拟合和欠拟合。偏差越小，方差对应增加模型的复杂性。随着参数越来越多添加到模型，模型复杂度上升和方差成为首要关注问题。如：更多的多项式项。偏差对应响应的负一阶导数。方差对应响应模型的复杂度。

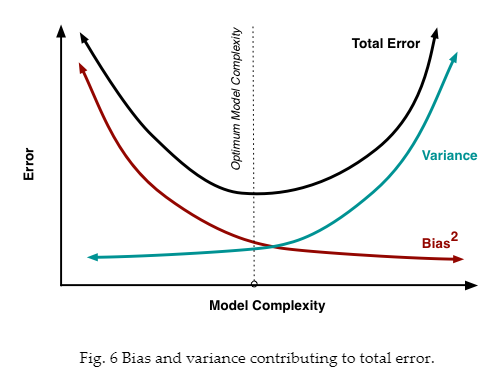
找一个点：

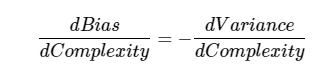
超过此点，过拟合，未到此点，欠拟合。要选整体误差最小的。

重采样，交叉验证。

文章来源：http://scott.fortmann-roe.com/docs/BiasVariance.html

处理偏差与方差

[Chǔlǐ piānchā yǔ fāngchā]

Process deviation and variance