BestCoder Round #40 解题报告

　　这场是第一场没有米的BC...

　　大概也是想震一震那些一听说没米了就不打BC的人吧

　　这次的题目质量比以往高了许多

　　（然而我并没有打这一场BC

　　但是今天下午到现在做的过程中真的学到了不少知识呢

---

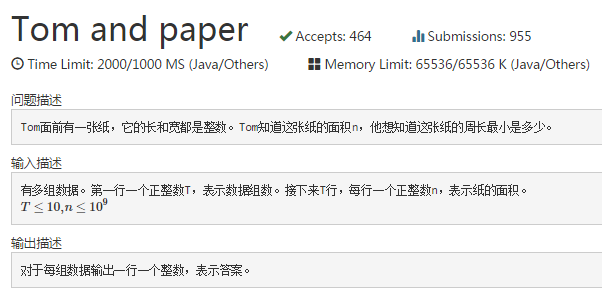
　　A题略水...

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<cmath>
 int T,n;
 int main(){
     scanf("%d",&T);
     while (T--){
         scanf("%d",&n);
         int tmp;
         for (int i=;i<=sqrt(n);i++) if (n%i==) tmp=i;
         printf("%d\n",*(n/tmp+tmp));
     }
     return ;
 }

---

　　然而第二题就不是非常简单的呢...

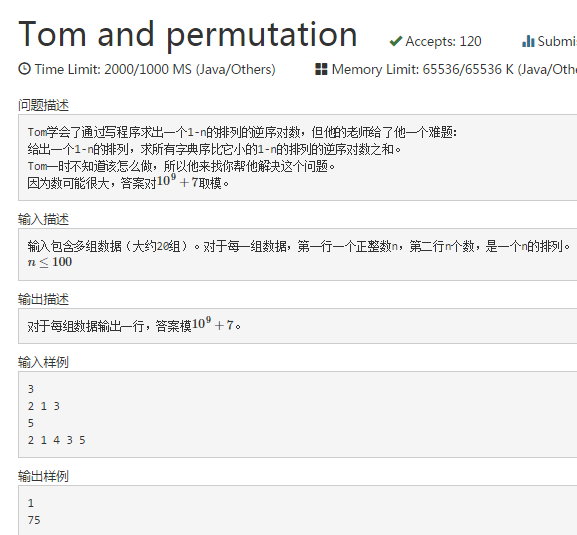
　　开始啊..我打算数位DP搞搞，然而突然发现排列是不能有重复数字的啊...

　　想到一个容易入手的状态 也就解决了这道题

　　我们需要让这些排列都小于读进来的排列

　　然后思考一下这些排列都有什么共性呢？

　　显然一定是由一段与排列相同的数字组成的前缀构成的，而接下来的一位一定小于排列，剩下的就随意了

　　这么一来好像问题就迎刃而解了

　　枚举与原串相同的位数（0~n-1），以及接下来一位的数字（小于原串该位置上的数字且在前面的位置中没出现过）

　　

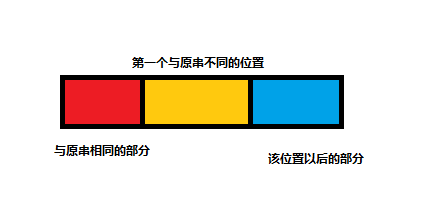
　　设当前枚举的黄色部分的位置为i，那么显然这样的字符串有(n-i)!种（即后面蓝色部分的n-i个数字的全排列）

　　这些字符串对答案的贡献分几部分考虑

　　1）红色部分内部的逆序对*(n-i)!，原串所有的前缀的逆序对数量可以通过树状数组预处理出

　　2）红色部分与黄色+蓝色部分的逆序对数，

可以用树状数组维护黄色+蓝色部分的值（即每向后走一格就将前一个数从树状数组中删去）

然后枚举红色部分的每一个元素，统计逆序对数，最后乘上(n-i)!

　　3）黄色部分与蓝色部分的逆序对数，直接与红色部分一样的答案最后-1即可（即把自己与自己减掉），

当然get的时候传参改成数值-1也是可以的

　　4）蓝色部分的逆序对数，这个在(n-i)!个字符串中都是不一样的，于是我们可以考虑总数

对于一个n个数的排列，我们考虑其中的两个数，它们成为逆序对的次数为C(n,2)*(n-2)!

所以逆序对总数为C(n,2)^2*(n-2)!

　　然后这道题就做完了，但是却对拍了一个下午都没找出哪里写错...

　　最后写两点做题过程中积累的东西吧...

　　1）C++的数组和Pas毕竟不一样...赋值啊什么的不能顶到maxn..而且居然本地不会出现RE

　　2）while not eof do 在C++里是以很奇怪的方式替代的呢...

 #include<cstdio>
 #include<cstdlib>
 #include<iostream>
 #include<cmath>
 #include<cstring>
 #define tt 1000000007
 #define maxn 110
 #define ll long long
 using namespace std;
 int n,a[maxn],tr[maxn];
 ll w[maxn],p[maxn],b[maxn];
 bool used[maxn];
 int get(int x){
     int tmp=;
     while (x) tmp+=tr[x],x-=x&(-x);
     return tmp;
 }
 void put(int x,int y){
     while (x<=n) tr[x]+=y,x+=x&(-x);
 }
 void build(){
     w[]=;for(int i=;i<maxn;i++) w[i]=(w[i-]*i)%tt;
     p[]=;for (int i=;i<maxn;i++) {
         ll tmp=i*(i-)/;
         p[i]=((tmp*tmp%tt)*w[i-])%tt;
     }
 }
 void solve(){
     ll ans=;
     memset(tr,,sizeof(tr));
     for (int i=;i<=n;i++) b[i]=(b[i-]+get(n-a[i]+))%tt,put(n-a[i]+,);
     memset(tr,,sizeof(tr));
     memset(used,true,sizeof(used));
     for (int i=;i<=n;i++) put(i,);
     for (int i=;i<=n;i++){
         if (i!=) put(a[i-],-),used[a[i-]]=false;
         for (int j=;j<a[i];j++) if (used[j]){
             ll tmp=b[i-];for (int k=;k<i;k++) tmp=(tmp+get(a[k]))%tt;
             if (j!=) tmp=(tmp+get(j-))%tt;
             tmp=((tmp*w[n-i])+p[n-i])%tt;
             ans=(ans+tmp)%tt;
         }
     }
     cout<<ans<<endl;
 }
 int main(){
     build();
     while (cin>>n){
         for (int i=;i<=n;i++) scanf("%d",a+i);
         solve();
     }
     return ;
 }

　　

---

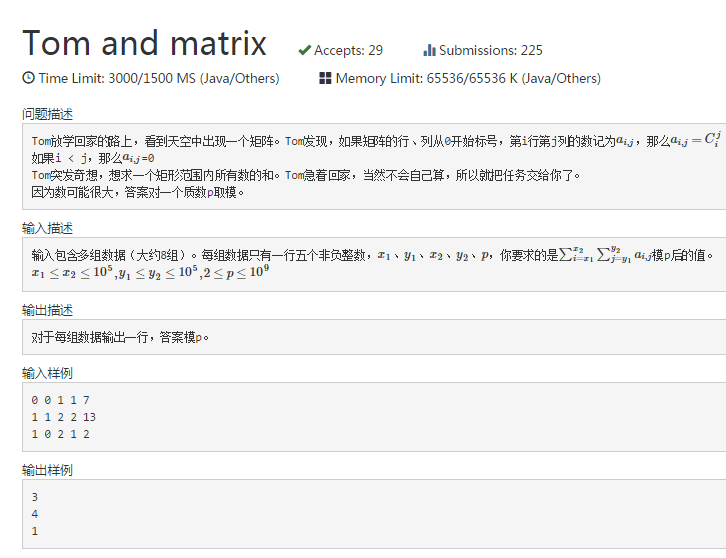
　　浓浓的数学味...于是又得去补充几个知识了呢

　　首先带取模的组合数是不能直接求解的...因为一旦C（n,m）中假设n>模数p，n!中就会出现p这个因子

　　然后C（n,m）就不可避地计算出了0...

　　这个时候要用到Lucas定理，递归定义　　

 ll lucas(int n,int m){
     if (m==) return ;
     if (n<tt&&m<tt) return c(n,m);
     return lucas(n/tt,m/tt)*lucas(n%tt,m%tt)%tt;
 }

　　另一个就是连续的组合数快速求解...

　　刚开始我一直在寻找同一行之间的关系..因为毕竟之前如果是整行是可以直接算的

　　然而实际上列存在着一定的关系

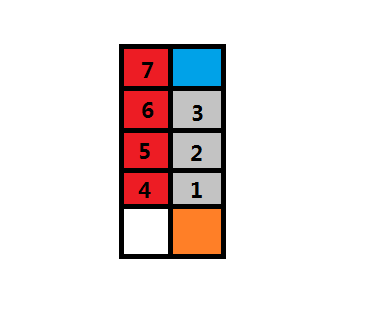
　　我们考虑这样一列上连续一段的求解（如图中红色部分）　　

　　根据杨辉三角的构造方法，C(n,m)=C(n-1,m)+C(n-1,m-1)

　　我们设4号格子的位置为（i,a）

　　最顶端红色格子的位置为（i,b）

　　C（a+1,i+1）=C(a,i)+C(a,i+1) → C(a,i)=C(a+1,i+1)-C(a,i+1)

　　显然...sigma（C（i,j））（a<=j<=b）=C（a+1,i+1）-C(b,i+1)

　　在图中也就是橙色格子-蓝色格子

　　然后对于每一列求解就可以了，但是要注意可能a,b不是真正的a,b

　　因为我们现在考虑的是建立在红色部分都至少为1的基础上的，于是对于每一列都要对行标号进行处理

　　另外还要注意，即使实际代表意义上不可能但取模意义下的减法可能会减出负的，也要处理

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #define maxn 100010
 #define ll long long
 int x1,y1,x2,y2,tt;
 ll fac[maxn],inv[maxn];
 int max(int a,int b){
     if (a>b) return a;
     return b;
 }
 ll mul(ll a,ll b){
     ll ans=,w=a;
     while (b){
         if (b%==) ans=ans*w%tt;
         w=w*w%tt;b=b>>;
     }
     return ans;
 }
 void build(){
     fac[]=;for (int i=;i<maxn;i++) fac[i]=fac[i-]*i%tt;
     inv[]=;for (int i=;i<maxn;i++) inv[i]=mul(fac[i],tt-);
 }
 ll c(int n,int m){
     return fac[n]*inv[m]%tt*inv[n-m]%tt;
 }
 ll lucas(int n,int m){
     if (m==) return ;
     if (n<tt&&m<tt) return c(n,m);
     return lucas(n/tt,m/tt)*lucas(n%tt,m%tt)%tt;
 }
 ll query(int n,int m){
     if (n<m) return ;
     return lucas(n,m);
 }
 void solve(){
     ll ans=;
     for (int i=y1;i<=y2;i++) {
         if (x2<i) continue;
         int l=max(x1,i),r=x2;
         if (l==i){l++;ans=(ans+)%tt;}
         ans=(ans+query(r+,i+)-query(l,i+)+tt)%tt;
     }
     printf("%lld\n",ans);
 }
 int main(){
     while (scanf("%d",&x1)!=EOF){
         scanf("%d%d%d%d",&y1,&x2,&y2,&tt);
         build();
         solve();
     }
     return ;
 }