矩阵快速幂 HDU 4565 So Easy!（简单？才怪！）

题目链接

题意：

　　

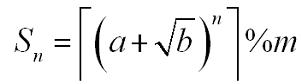
思路：

　　直接拿别人的图，自己写太麻烦了~

　　

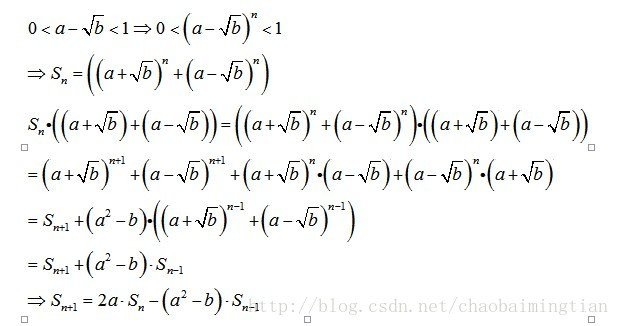
　　然后就可以用矩阵快速幂套模板求递推式啦~

另外：

　　这题想不到或者不会矩阵快速幂，根本没法做，还是2013年长沙邀请赛水题，也是2008年Google Codejam Round 1A的C题。

#include <bits/stdc++.h>

typedef long long ll;
const int N = 5;
int a, b, n, mod;
/*
	*矩阵快速幂处理线性递推关系f(n)=a1f(n-1)+a2f(n-2)+...+adf(n-d)
*/
struct Matrix {
    int row, col;
    ll arr[N][N];
    Matrix(int r=0, int c=0) {
        row = r; col = c;
        memset (arr, 0, sizeof (arr));
    }
    Matrix operator * (const Matrix &B) {
        Matrix ret(row, B.col);
        for (int i=0; i<row; ++i) {
            for (int j=0; j<B.col; ++j) {
                for (int k=0; k<col; ++k) {
                    ret.arr[i][j] = (ret.arr[i][j] + (ll) arr[i][k] * B.arr[k][j]) % mod;
                }
            }
        }
        return ret;
    }
    void unit(int n) {
        row = col = n;
        for (int i=0; i<n; ++i) {
            arr[i][i] = 1;
        }
    }
};
Matrix operator ^ (Matrix X, ll n) {
    Matrix ret; ret.unit (X.col);
    while (n) {
        if (n & 1) {
            ret = ret * X;
        }
        X = X * X;
        n >>= 1;
    }
    return ret;
}

int f[3], x[3];

int main() {
    while (scanf ("%d%d%d%d", &a, &b, &n, &mod) == 4) {
        double c = (double) a + sqrt ((double) b);
        f[1] = ((ll) ceil (c)) % mod;
        f[2] = ((ll) ceil (c*c)) % mod;
        int d = 2;
        x[1] = (2*a) % mod; x[2] = (-(a*a-b) % mod + mod) % mod;

        if (n <= d) {
            printf ("%d\n", f[n]);
        } else {
            Matrix Fn(d+1, d+1), Fd(d+1, 1);
            for (int i=0; i<Fn.row-1; ++i) {
                Fn.arr[i][i+1] = 1;
            }
            for (int i=1; i<Fn.col; ++i) {
                Fn.arr[Fn.row-1][i] = x[d-i+1];
            }
            for (int i=0; i<Fd.row; ++i) {
                Fd.arr[i][0] = f[i];
            }
            Fn = Fn ^ (n - d);
            Fn = Fn * Fd;
            printf ("%d\n", Fn.arr[d][0]);
        }
    }
    return 0;
}