AC自动机算法

AC自动机简介： 

首先简要介绍一下AC自动机：Aho-Corasick automation，该算法在1975年产生于贝尔实验室，是著名的多模匹配算法之一。一个常见的例子就是给出n个单词，再给出一段包含m个字符的文 章，让你找出有多少个单词在文章里出现过。要搞懂AC自动机，先得有字典树Trie和KMP模式匹配算法的基础知识。KMP算法是单模式串的字符匹配算 法，AC自动机是多模式串的字符匹配算法。

AC自动机的构造：

1.构造一棵Trie，作为AC自动机的搜索数据结构。

2.构造fail指针，使当前字符失配时跳转到具有最长公共前后缀的字符继续匹配。如 同 KMP算法一样， AC自动机在匹配时如果当前字符匹配失败，那么利用fail指针进行跳转。由此可知如果跳转，跳转后的串的前缀，必为跳转前的模式串的后缀并且跳转的新位 置的深度（匹配字符个数）一定小于跳之前的节点。所以我们可以利用 bfs在 Trie上面进行 fail指针的求解。

3.扫描主串进行匹配。

AC自动机详讲：

我们给出5个单词，say，she，shr，he，her。给定字符串为yasherhs。问多少个单词在字符串中出现过。

一、Trie

首先我们需要建立一棵Trie。但是这棵Trie不是普通的Trie，而是带有一些特殊的性质。

首先会有3个重要的指针，分别为p, p->fail, temp。

1.指针p，指向当前匹配的字符。若p指向root，表示当前匹配的字符序列为空。（root是Trie入口，没有实际含义）。

2.指针p->fail，p的失败指针，指向与字符p相同的结点，若没有，则指向root。

3.指针temp，测试指针（自己命名的，容易理解！~），在建立fail指针时有寻找与p字符匹配的结点的作用，在扫描时作用最大，也最不好理解。

对于Trie树中的一个节点，对应一个序列s[1...m]。此时，p指向字符s[m]。若在下一个字符处失配，即p->next[s[m+1]] == NULL，则由失配指针跳到另一个节点(p->fail)处，该节点对应的序列为s[i...m]。若继续失配，则序列依次跳转直到序列为空或出现 匹配。在此过程中，p的值一直在变化，但是p对应节点的字符没有发生变化。在此过程中，我们观察可知，最终求得得序列s则为最长公共后缀。另外，由于这个 序列是从root开始到某一节点，则说明这个序列有可能是某些序列的前缀。

再次讨论p指针转移的意义。如果p指针在某一字符s[m+1]处失配(即p->next[s[m+1]] == NULL)，则说明没有单词s[1...m+1]存在。此时，如果p的失配指针指向root，则说明当前序列的任意后缀不会是某个单词的前缀。如果p的失 配指针不指向root，则说明序列s[i...m]是某一单词的前缀，于是跳转到p的失配指针，以s[i...m]为前缀继续匹配s[m+1]。

对于已经得到的序列s[1...m]，由于s[i...m]可能是某单词的后缀，s[1...j]可能是某单词的前缀，所以s[1...m]中可能会出现 单词。此时，p指向已匹配的字符，不能动。于是，令temp = p，然后依次测试s[1...m], s[i...m]是否是单词。

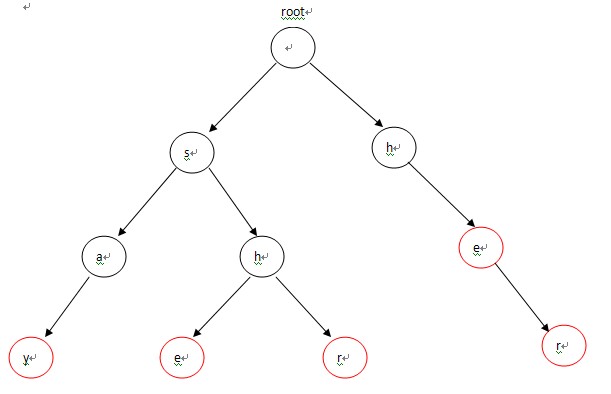
构造的Trie为：

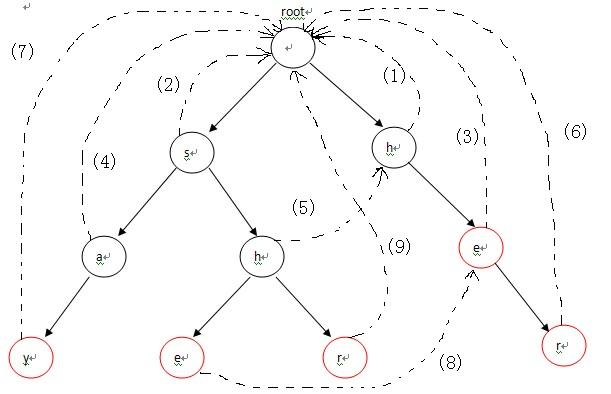
二、构造失败指针

用BFS来构造失败指针，与KMP算法相似的思想。

首先，root入队，第1次循环时处理与root相连的字符，也就是各个单词的第一个字符h和s，因为第一个字符不匹配需要重新匹配，所以第一个字符都指
向root（root是Trie入口，没有实际含义）失败指针的指向对应下图中的(1)，(2)两条虚线；第2次进入循环后，从队列中先弹出h，接下来p
指向h节点的fail指针指向的节点，也就是root；p=p->fail也就是p=NULL说明匹配序列为空，则把节点e的fail指针指向
root表示没有匹配序列，对应图-2中的(3)，然后节点e进入队列；第3次循环时，弹出的第一个节点a的操作与上一步操作的节点e相同，把a的
fail指针指向root，对应图-2中的(4)，并入队；第4次进入循环时，弹出节点h(图中左边那个)，这时操作略有不同。由于
p->next[i]!=NULL(root有h这个儿子节点，图中右边那个)，这样便把左边那个h节点的失败指针指向右边那个root的儿子节点
h，对应图-2中的(5)，然后h入队。以此类推：在循环结束后，所有的失败指针就是图-2中的这种形式。

三、扫描

构造好Trie和失败指针后，我们就可以对主串进行扫描了。这个过程和KMP算法很类似，但是也有一定的区别，主要是因为AC自动机处理的是多串模式，需要防止遗漏某个单词，所以引入temp指针。

匹配过程分两种情况：(1)当前字符匹配，表示从当前节点沿着树边有一条路径可以到达目标字符，此时只需沿该路径走向下一个节点继续匹配即可，目标
字符串指针移向下个字符继续匹配；(2)当前字符不匹配，则去当前节点失败指针所指向的字符继续匹配，匹配过程随着指针指向root结束。重复这2个过程
中的任意一个，直到模式串走到结尾为止。

对照上图，看一下模式匹配这个详细的流程，其中模式串为yasherhs。对于i=0,1。Trie中没有对应的路径，故不做任何操
作；i=2,3,4时，指针p走到左下节点e。因为节点e的count信息为1，所以cnt+1，并且讲节点e的count值设置为-1，表示改单词已经
出现过了，防止重复计数，最后temp指向e节点的失败指针所指向的节点继续查找，以此类推，最后temp指向root，退出while循环，这个过程中
count增加了2。表示找到了2个单词she和he。当i=5时，程序进入第5行，p指向其失败指针的节点，也就是右边那个e节点，随后在第6行指向r
节点，r节点的count值为1，从而count+1，循环直到temp指向root为止。最后i=6,7时，找不到任何匹配，匹配过程结束。