用turtle库显示汉诺塔问题的过程

　　　　　　　　　　　　　用turtle库显示汉诺塔问题的过程　　

一、什么是汉诺塔问题？

　　　一座汉诺塔，塔内有3个座A、B、C，A座上有n个盘子，盘子大小不等，大的在下，小的在上，如图所示。把这n个盘子从A座移到C座，但每次只能移动一个盘子，并且自移动过程中，3个座上的盘子始终保持大盘在下，小盘在上。在移动过程中可以利用B座来放盘子。‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‪

‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‪‬

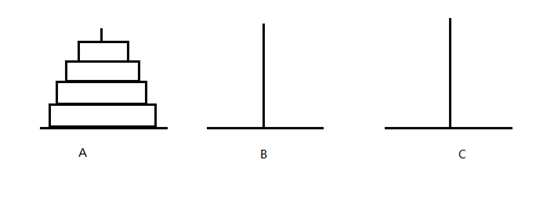
二、静态的方法

1、代码如下：

　　

 def func(n,A,B,C):
     if n== 1:
         print(A,'-->',C)
     else:
         func(n-1,A,C,B)
         func(1,A,B,C)
         func(n-1,B,A,C)
 num = input()
 func(int(num),'A','B','C')

2、运行结果如下：

　　

　　　　这是一个静态过程。

三、动态过程

1、用turtle库的代码如下：

　　

 import turtle

 class Stack:
     def __init__(self):
         self.items = []
     def isEmpty(self):
         return len(self.items) == 0
     def push(self, item):
         self.items.append(item)
     def pop(self):
         return self.items.pop()
     def peek(self):
         if not self.isEmpty():
             return self.items[len(self.items) - 1]
     def size(self):
         return len(self.items)

 def drawpole_3():#画出汉诺塔的poles
     t = turtle.Turtle()
     t.hideturtle()
     def drawpole_1(k):
         t.up()
         t.pensize(10)
         t.speed(100)
         t.goto(400*(k-1), 100)
         t.down()
         t.goto(400*(k-1), -100)
         t.goto(400*(k-1)-20, -100)
         t.goto(400*(k-1)+20, -100)
     drawpole_1(0)#画出汉诺塔的poles[0]
     drawpole_1(1)#画出汉诺塔的poles[1]
     drawpole_1(2)#画出汉诺塔的poles[2]

 def creat_plates(n):#制造n个盘子
     plates=[turtle.Turtle() for i in range(n)]
     for i in range(n):
         plates[i].up()
         plates[i].hideturtle()
         plates[i].shape("square")
         plates[i].shapesize(1,8-i)
         plates[i].goto(-400,-90+20*i)
         plates[i].showturtle()
     return plates

 def pole_stack():#制造poles的栈
     poles=[Stack() for i in range(3)]
     return poles

 def moveDisk(plates,poles,fp,tp):#把poles[fp]顶端的盘子plates[mov]从poles[fp]移到poles[tp]
     mov=poles[fp].peek()
     plates[mov].goto((fp-1)*400,150)
     plates[mov].goto((tp-1)*400,150)
     l=poles[tp].size()#确定移动到底部的高度（恰好放在原来最上面的盘子上面）
     plates[mov].goto((tp-1)*400,-90+20*l)

 def moveTower(plates,poles,height,fromPole, toPole, withPole):#递归放盘子
     if height >= 1:
         moveTower(plates,poles,height-1,fromPole,withPole,toPole)
         moveDisk(plates,poles,fromPole,toPole)
         poles[toPole].push(poles[fromPole].pop())
         moveTower(plates,poles,height-1,withPole,toPole,fromPole)

 myscreen=turtle.Screen()
 drawpole_3()
 n=int(input("请输入汉诺塔的层数并回车:\n"))
 plates=creat_plates(n)
 poles=pole_stack()
 for i in range(n):
     poles[0].push(i)
 moveTower(plates,poles,n,0,2,1)
 myscreen.exitonclick()

　　这是我从网上找来的动态过程的程序。我输入的层数为5层

2、运行的过程如下：

因为我自己拍的视频传不上来，所以我就去网上找了一个视频，而且刚好都是5层。视频链接如下：

https://www.bilibili.com/video/av38671130/?p=1

　

这是我用电脑截的图：　　

　　　　

　　　　

　　

　

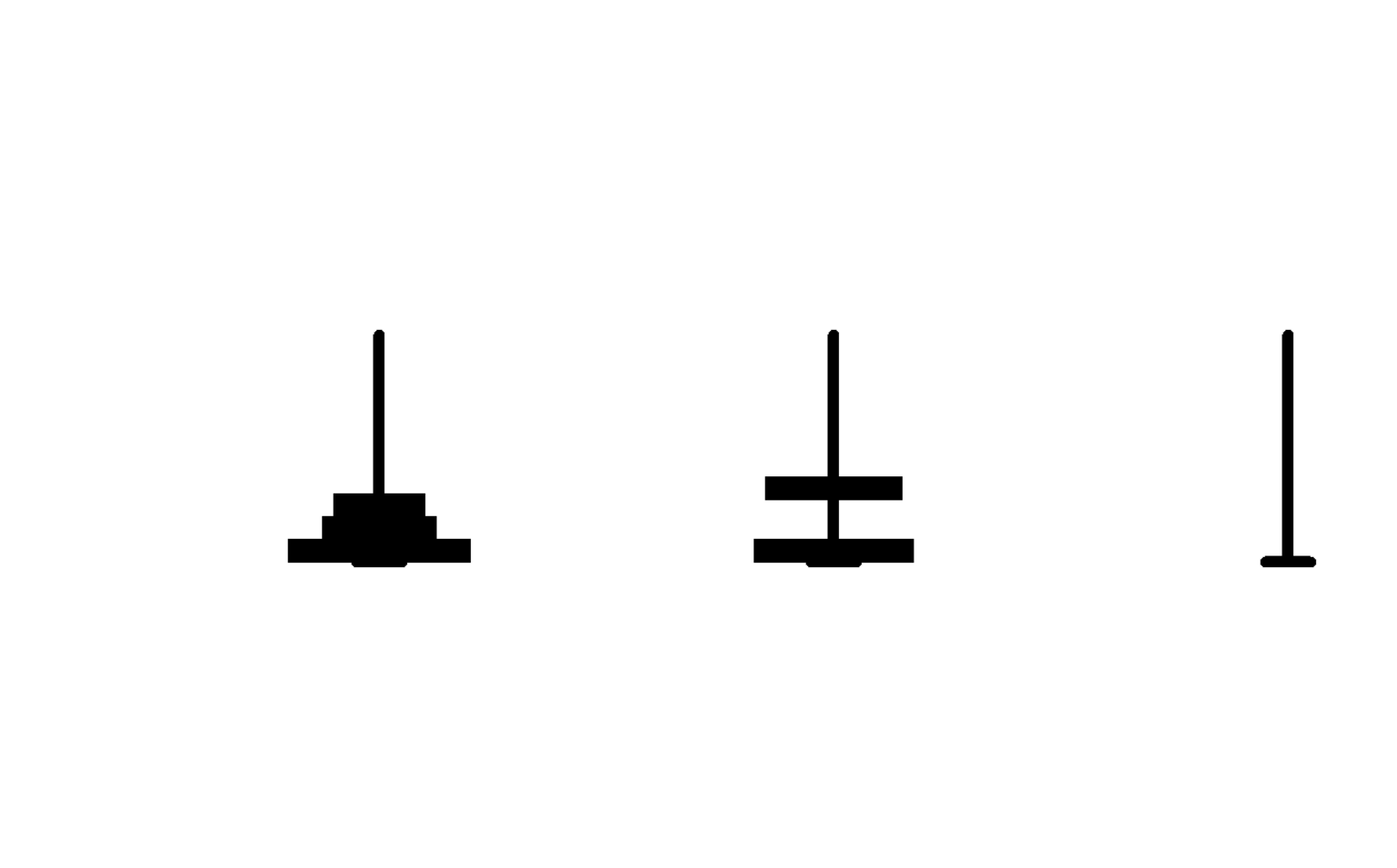
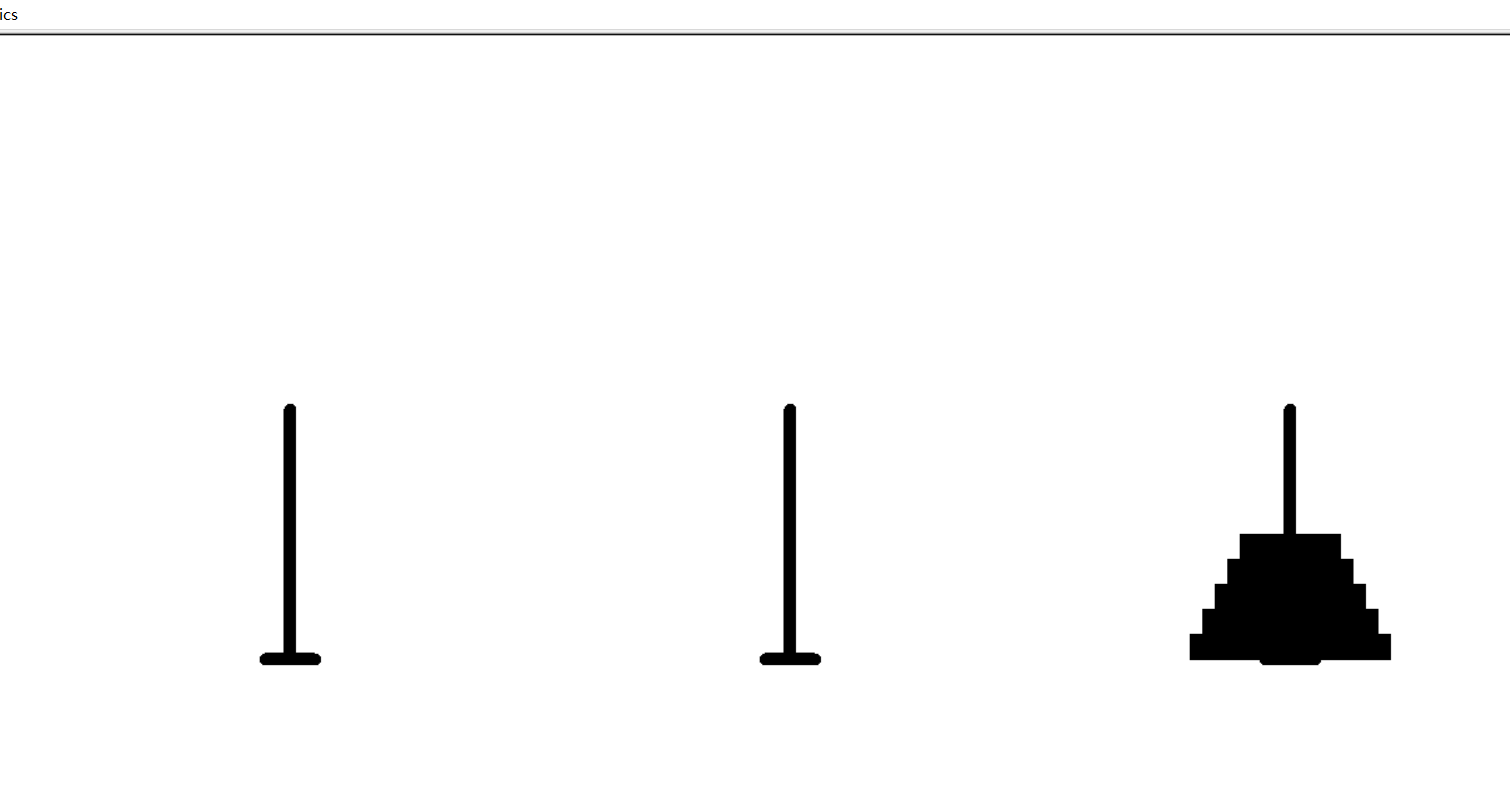
　到这里运行的过程就结束啦~~~~