凸包算法（Graham扫描法）详解

先说下基础知识，不然不好理解后面的东西

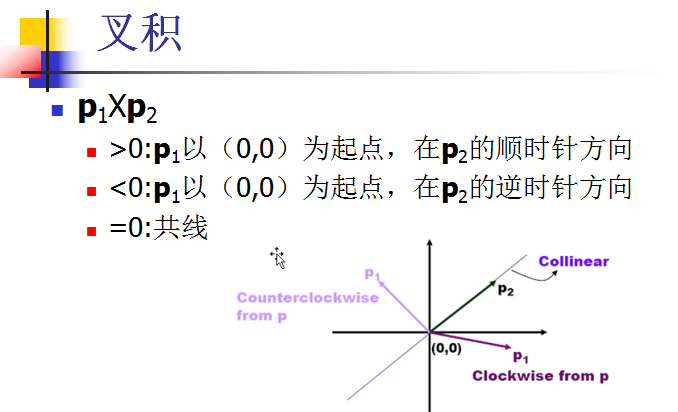
两向量的X乘p1(x1,y1),p2(x2,y2)

p1Xp2如果小于零则说明  p1在p2的逆时针方向

如果大于零则说明 p1在p2的顺时针方向

struct node{
    double x,y;
    node friend operator -(node a,node b)//对减法符号进行重载
    {
        return {a.x-b.x,a.y-b.y};
    }
}p[],s[];
double X(node a,node b){
    return a.x*b.y-a.y*b.x;
}

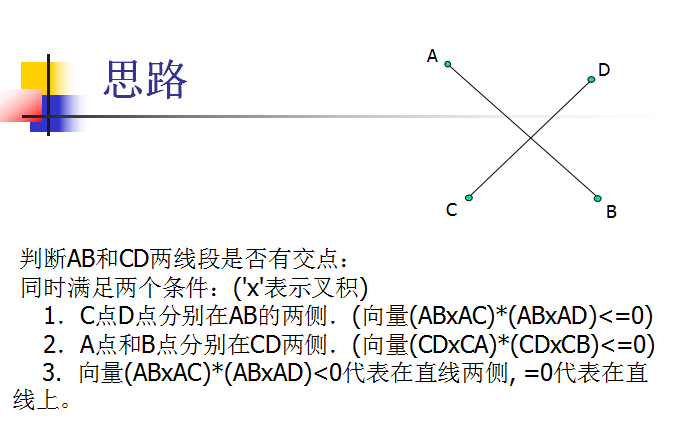
这个方法很有用处。比如判断一个点是否在一条线段的左边还是右边，可以用X乘来判断，或者判断两条线段是否相交

接着说说凸包    Graham扫描法

1.在平面上一些散乱的点，首先  找找到这些点中处于最左下方的点

        for(int i=;i<=N;i++)
        cin>>p[i].x>>p[i].y;
        int k=;
        for(int i=;i<=N;i++)
        {
            if(p[i].y<p[k].y||(p[k].y==p[i].y&&p[i].x<p[k].x))
            k=i;
        }
        swap(p[],p[k]);        

2.对这些点进行排序。把按照极角(polar angle)从小到大排序(以 p1为极点)，极角相同的点按照到的距离从小到大排序。

int cmp(node a,node b)
{
    double x=X(a-p[],b-p[]);//以p[1]为极点，通过X乘来判断 

    if(x>) return ;//让a处于b的顺时针
    if(x==&&dis(a,p[])<dis(b,p[]))return ;//角度相同看距离
    return ;
}

sort(p+,p+N+,cmp);

3.再开一个结构体数组s 来储存凸包最外围的点，也就是结果，这个有点容易让人搞迷。

遍历剩下的点,while循环把发现不是凸包顶点的点移除出去，因为当逆时针遍历凸包时，我们应该在每个顶点向左转。因此当while循环发现在一个顶点处没有向左转时，就把该顶点移除出去。

至于如何判断向左向右则是根据叉积来判断，前面我们已经解决过这个问题了

double multi(node a,node b,node c)
{
    return X(b-a,c-a);
}

   　　 s[]=p[];
        s[]=p[];
        int t=;
        for(int i=;i<=N;i++)
        {
            // 发现在栈里边一个顶点处没有向左转时，就把该顶点移除出去
            while(t>=&&multi(s[t-],s[t],p[i])<=) t--;
            s[++t]=p[i];
        }

这个是求凸包的周长的

hdu1392    http://acm.hdu.edu.cn/showproblem.php?pid=1392

算是模板题吧

#include<bits/stdc++.h>
using namespace std;

struct point{
    double x,y;
    point friend operator -(point a,point b)
    {return {a.x-b.x,a.y-b.y};}
}p[],s[];
double dis(point a,point b)
{
    point c=a-b;
    return sqrt(c.x*c.x+c.y*c.y);
}
double X(point a,point b)
{
    return a.x*b.y-a.y*b.x;
}
int cmp(point a,point b)
{
    double x=X(a-p[],b-p[]);

    if(x>) return ;
    if(x==&&dis(a,p[])<dis(b,p[])) return ;
    return ;
}
double multi(point p1,point p2,point p3)
{
    return X(p2-p1,p3-p1);
}
int main()
{
    int N;
    while(scanf("%d",&N),N)
    {
        for(int i=;i<=N;i++) cin>>p[i].x>>p[i].y;

        if(N==)
        {
            printf("0.00\n");
            continue;
        }
        else if(N==)
        {
            printf("%.2lf\n",dis(p[],p[]));
            continue;
        }

        int k=;
        for(int i=;i<=N;i++)
        if(p[i].y<p[k].y||(p[i].y==p[k].y&&p[i].x<p[k].x))k=i;
        swap(p[],p[k]);

        sort(p+,p++N,cmp);

        s[]=p[];
        s[]=p[];
        int t=;
        for(int i=;i<=N;i++)
        {
            while(t>=&&multi(s[t-],s[t],p[i])<=) t--;
            s[++t]=p[i];
        }
        double sum=;
        for(int i=;i<t;i++)
        {
            sum+=dis(s[i],s[i+]);
        }
        printf("%.2lf\n",sum+dis(s[],s[t]));
    }
    return ;
}

emmm  再来个求任意多边形的面积

struct Point {
    double x, y;
};

//计算任意多边形的面积，顶点按照顺时针或者逆时针方向排列
double polygon_area(Point *p, int n)
{
    if(n < ) return ;

    double sum = ;
    p[n + ] = p[];
    for(int i = ; i <= n; i++)
        sum += p[i].x * p[i + ].y - p[i].y * p[i + ].x;//可以理解为不管这个多边形在哪，都以原点为分割点，就算原点在外面也可以算出，因为有正负可以抵消掉多余的
    sum = fabs(sum / 2.0);
    return sum;
}

再来个求面积均匀的多边形重心

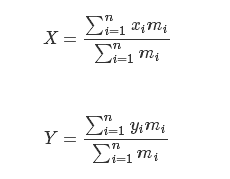
需要把多边形以p[0]为分界点  分成n-2个三角形，求出这些三角形的重心（i,j），乘以该三角形的面积，如上图公式

#include<bits/stdc++.h>
using namespace std;
struct node{
    double x,y;
    node friend operator -(node a,node b)
    {
        return {a.x-b.x,a.y-b.y};
    }
    double friend operator *(node a,node b)//对*进行重载  node*node 相当于X乘
    {
        return a.x*b.y-a.y*b.x;
    }
}a[];
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        int n;
        cin>>n;
        for(int i=;i<=n;i++) cin>>a[i].x>>a[i].y;

        double S=,X=,Y=;
        for(int i=;i<n;i++)
        {
            double x=(a[i]-a[])*(a[i+]-a[]);//这个乘和下面的不一样，这时X乘，求出三角形面积
            X+=(a[].x+a[i].x+a[i+].x)*x;//重心（没除以3）乘以面积
            Y+=(a[].y+a[i].y+a[i+].y)*x;
            S+=x;
        }
        printf("%.2lf %.2lf\n",X/S/(double),Y/S/(double));//除以3为重心
     }
    return ;
}