CodeForces527D. Fuzzy Search

time limit per test：3 seconds　　memory limit per test：256 megabytes

input：standard input

output：standard output

Leonid works for a small and promising start-up that works on decoding the human genome. His duties include solving complex problems of finding certain patterns in long strings consisting of letters 'A', 'T', 'G' and 'C'.

Let's consider the following scenario. There is a fragment of a human DNA chain, recorded as a string S. To analyze the fragment, you need to find all occurrences of string T in a string S. However, the matter is complicated by the fact that the original chain fragment could contain minor mutations, which, however, complicate the task of finding a fragment. Leonid proposed the following approach to solve this problem.

Let's write down integer k ≥ 0 — the error threshold. We will say that string T occurs in string S on position i (1 ≤ i ≤ |S| - |T| + 1), if after putting string T along with this position, each character of string T corresponds to the some character of the same value in string S at the distance of at most k. More formally, for any j (1 ≤ j ≤ |T|) there must exist such p (1 ≤ p ≤ |S|), that |(i + j - 1) - p| ≤ k and S[p] = T[j].

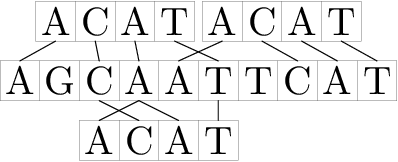
For example, corresponding to the given definition, string "ACAT" occurs in string "AGCAATTCAT" in positions 2, 3 and 6.

Note that at k = 0 the given definition transforms to a simple definition of the occurrence of a string in a string.

Help Leonid by calculating in how many positions the given string T occurs in the given string S with the given error threshold.

Input

The first line contains three integers |S|, |T|, k (1 ≤ |T| ≤ |S| ≤ 200 000, 0 ≤ k ≤ 200 000) — the lengths of strings S and T and the error threshold.

The second line contains string S.

The third line contains string T.

Both strings consist only of uppercase letters 'A', 'T', 'G' and 'C'.

Output

Print a single number — the number of occurrences of T in S with the error threshold k by the given definition.

Examples

input

10 4 1
AGCAATTCAT
ACAT

output

Note

If you happen to know about the structure of the human genome a little more than the author of the problem, and you are not impressed with Leonid's original approach, do not take everything described above seriously.

Solution

只要A串中[i-k,i+k]范围内有字符X，就认为i位置可以匹配字符X。

问有多少位置可以匹配目标串B

生成函数 FFT

注意到只有四种字符，那么可以暴力分别处理这四种字符。

对于每种字符，在A串中扫描出可以匹配它的所有位置，标记为1，再将B串反转，将B串上对应字符的位置也标记为1，卷积即可得到该种字符的匹配情况。

做四遍卷积就可以愉快出解了。

 /*by SilverN*/

 #include<iostream>

 #include<algorithm>

 #include<cstring>

 #include<cstdio>

 #include<cmath>

 #include<vector>

 #define LL long long

 using namespace std;

 const double pi=acos(-1.0);

 const int mxn=;

 int read(){

     int x=,f=;char ch=getchar();

     while(ch<'' || ch>''){if(ch=='-')f=-;ch=getchar();}

     while(ch>='' && ch<=''){x=x*+ch-'';ch=getchar();}

     return x*f;

 }

 struct com{

     double x,y;

     com operator + (const com &b){return (com){x+b.x,y+b.y};}

     com operator - (const com &b){return (com){x-b.x,y-b.y};}

     com operator * (const com &b){return (com){x*b.x-y*b.y,x*b.y+y*b.x};}

     com operator / (double v){return (com){x/v,y/v};}

 }a[mxn<<],b[mxn<<];

 int N,len;

 int rev[mxn<<];

 void FFT(com *a,int flag){

     for(int i=;i<N;i++)

         if(i<rev[i])swap(a[i],a[rev[i]]);

     for(int i=;i<N;i<<=){

         com wn=(com){cos(pi/i),flag*sin(pi/i)};

         int p=i<<;

         for(int j=;j<N;j+=p){

             com w=(com){,};

             for(int k=;k<i;k++,w=w*wn){

                 com x=a[j+k],y=w*a[j+k+i];

                 a[j+k]=x+y;

                 a[j+k+i]=x-y;

             }

         }

     }

     if(flag==-)for(int i=;i<N;i++) a[i].x/=N;

     return;

 }

 char s[mxn],c[mxn];

 int S,T,K;

 LL ans[mxn<<];

 int hd,tl,ct;

 void solve(char tp){

     memset(a,,sizeof a);

     memset(b,,sizeof b);

     hd=;tl=-;ct=;

     int i,j;

     for(i=;i<S;i++){

         while(i-hd>K){if(s[hd]==tp)ct--;hd++;}

         while(tl-i+<=K && tl<S){tl++;if(s[tl]==tp)ct++;}

         if(ct>) a[i].x=;

     }

     for(i=;i<T;i++)

         if(c[i]==tp) b[i].x=;

     FFT(a,);FFT(b,);

     for(i=;i<N;i++) a[i]=a[i]*b[i];

     FFT(a,-);

     for(i=;i<N;i++)ans[i]+=(LL)(a[i].x+0.5);

     return;

 }

 int main(){

     int i,j;

     S=read();T=read();K=read();

     scanf("%s",s);scanf("%s",c);

     int m=S+T;

     for(N=,len=;N<=m;N<<=)len++;

     for(i=;i<N;i++)

         rev[i]=(rev[i>>]>>)|((i&)<<(len-));

     reverse(c,c+T);

     solve('A');

     solve('G');

     solve('C');

     solve('T');

     int res=;

     for(i=;i<N;i++){

         if(ans[i]==T)res++;

 //        printf("%lld\n",ans[i]);

     }

     printf("%d\n",res);

     return ;

 }