AVL树 算法思想与代码实现

AVL树是高度平衡的二叉搜索树，按照二叉搜索树（Binary Search Tree）的性质，AVL首先要满足：

若它的左子树不为空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不为空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉搜索树。

AVL树的性质：

1. 左子树和右子树的高度之差的绝对值不超过1
2. 树中的每个左子树和右子树都是AVL树
3. 每个节点都有一个平衡因子(balance factor--bf),任一节点的平衡因子是-1,0,1之一

(每个节点的平衡因子bf 等于右子树的高度减去左子树的高度 )    

构建AVL树节点

////	AVL树的节点类
template<class K,class V>
class AVLTreeNode
{
	K _key;
	V _value;
	int  _bf;//平衡因子 -1,0,1(每个节点的平衡因子等于右子树的高度减去左子树的高度)
	AVLTreeNode<K, V>* _parent;	//指向父节点的指针
	AVLTreeNode<K, V>* _left;			//指向左孩子的指针
	AVLTreeNode<K, V>* _right;		//指向右孩子的指针

	AVLTreeNode(const K& key = K(), const V& value = V())
		:_key(key)
		, _value(value)
		, _bf(0)
		, _parent(NULL)
		, _left(NULL)
		, _right(NULL)
	{}
};

插入数据：

插入数据以后，父节点的平衡因子必然会被改变！

首先判断父节点的平衡因子是否满足性质1（-1<= parent->_bf <=1），如果满足，则要回溯向上检查插入该节点是否影响了其它节点的平衡因子值！

• 当父节点的平衡因子等于0时，父节点所在的子树已经平衡，不会影响其他节点的平衡因子了。
• 当父节点的平衡因子等于1或者-1时，需要继续向上回溯一层，检验祖父节点的平衡因子是否满足条件（把父节点给当前节点）。
• 当父节点的平衡因子等于2或者-2时，不满足性质1，这时需要进行旋转 来降低高度 ：   

旋转的目的是为了降低高度

旋转的一般形态：

旋转至少涉及三层节点，所以至少要向上回溯一层 ，才会发现非法的平衡因子并进行旋转

向上回溯校验时，需要进行旋转的几种情况：

1. 当前节点的父节点的平衡因子等于2时，说明父节点的右树比左树高：

• 这时如果当前节点的平衡因子等于1，那么当前节点的右树比左树高，形如“ \ ”，需要进行左旋；
• 如果当前节点的平衡因子等于-1，那么当前节点的右树比左树低，形如“ > ”，需要进行右左双旋！

2. 当前节点的父节点的平衡因子等于-2时，说明父节点的右树比左树低：

• 这时如果当前节点的平衡因子等于-1，那么当前节点的右树比左树低，形如“ / ”,需要进行右旋；
• 如果当前节点的平衡因子等于1，那么当前节点的右树比左树高，形如“ < ”,需要进行左右双旋！

//  AVLTree插入算法
template<class K, class V>
bool AVLTree<K,V>::Insert(const K& key, const V& value)
{
	//1.空树
	if (_root == NULL)
	{
		_root = new AVLTreeNode<K, V>(key, value);
		return true;
	}

	//2.AVL树不为NULL
	AVLTreeNode<K, V>* parent = NULL;
	AVLTreeNode<K, V>* cur = _root;
	//找到数据插入位置
	while (cur)
	{
		if (cur->_key < key)
		{
			parent = cur;
			cur = cur->_right;
		}
		else	if (cur->_key > key)
		{
			parent = cur;
			cur = cur->_left;
		}
		else
		{
			return false;
		}
	}
	//插入数据
		cur = new AVLTreeNode<K, V>(key, value);
		cur->_parent = parent;
		if (parent->_key > key)
			parent->_left = cur;
		else
			parent->_right = cur;

		while (parent)
		{
			//更新平衡因子
			if (cur == parent->_left)
				parent->_bf--;
			else if (cur == parent->_right)
				parent->_bf++;

			//检验平衡因子是否合法
			if (parent->_bf == 0)
				break;
			else if (parent->_bf == -1 || parent->_bf == 1)
			{	// 回溯上升 更新祖父节点的平衡因子并检验合法性
				cur = parent;
				parent = cur->_parent;
			}
			else   //	2 -2 平衡因子不合法 需要进行旋转 降低高度
			{
				if (parent->_bf == 2)
				{
					if (cur->_bf == 1)
						_RotateL(parent);
					else
						_RotateRL(parent);
				}
				else if (parent->_bf == -2)
				{
					if (cur->_bf == -1)
						_RotateR(parent);
					else
						_RotateLR(parent);
				}
				break;
			}
		}
}

　　　

---

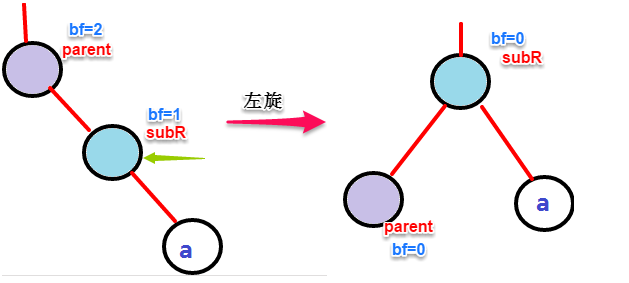
左旋的两种情况：

1.parent有两个孩子：没有插入节点c之前处于平衡状态，插入c之后，平衡被破坏，向上回溯检验祖父节点的平衡因子，当其bf=2 时，以此节点为轴进行左旋

2.parent有一个孩子：没有插入节点a之前处于平衡状态，插入节点a之后，parent节点的平衡因子bf=2不满足AVL树的性质，要以parent为轴进行左旋

//左旋
template<class K, class V>
void AVLTree<K, V>::_RotateL(AVLTreeNode<K, V>*&  parent)
{
	AVLTreeNode<K, V>* subR = parent->_right;
	AVLTreeNode<K, V>* subRL = subR->_left;
	AVLTreeNode<K, V>* ppNode = parent->_parent;		//标记祖先节点

	//1.构建parent子树 链接parent和subRL
	parent->_right = subRL;
	if (subRL) subRL->_parent = parent;
	//2.构建subR子树 链接parent和subR
	subR->_left = parent;
	parent->_parent = subR;
	//3.链接祖先节点和subR节点
	subR->_parent = ppNode;
	if (ppNode== NULL)
	{//如果祖先节点为NULL，说明目前的根节点为subR
		_root = subR;
	}
	else
	{	//将祖先节点和subR节点链接起来
		if (parent == ppNode->_left)
			ppNode->_left = subR;
		else
			ppNode->_right = subR;
	}
	//4.重置平衡因子
	parent->_bf = 0;
	subR->_bf = 0;
	//5.更新subR为当前父节点
	parent = subR;
}

　　

---

右旋的两种情况：

1. parent既有左孩子又有右孩子：插入c之前处于平衡态，插入c之后parent的平衡因子变为-2，这时要以parent为轴进行旋转

2. parent只有一个孩子：插入a之前处于平衡状态，插入之后subL与parent的平衡因子被改变，需要以parent为轴进行旋转

///右旋
template<class K, class V>
void AVLTree<K, V>::_RotateR(AVLTreeNode<K, V>*&  parent)
{
	AVLTreeNode<K, V>* subL = parent->_left;
	AVLTreeNode<K, V>* subLR = subL->_right;
	AVLTreeNode<K, V>* ppNode = parent->_parent;		//标记祖先节点
	//1.构建parent子树 将parent和subLR链接起来
	parent->_left = subLR;
	if (subLR) subLR->_parent = parent;
	//2.构建subL子树 将subL与parent链接起来
	subL->_right = parent;
	parent->_parent = subL;
	//3.将祖先节点与sunL链接起来
	if (ppNode == NULL)
	{	//如果祖先为NULL，说明当前subL节点为根节点
		subL->_parent = NULL;
		_root = subL;
	}
	else
	{
		subL->_parent = ppNode;
		if (ppNode->_left == parent)
			ppNode->_left = subL;
		else if (ppNode->_right == parent)
			ppNode->_right = subL;
	}
	//4.重置平衡因子
	parent->_bf = 0;
	subL->_bf = 0;
	//5.更新subL为当前父节点
	parent = subL;
}

　

---

 左右双旋：

1. parent只有一个孩子：在插入节点sunLR之前，AVL树处于平衡状态，左右子树高度差的绝对值不超过1。

　　由于插入了节点subLR导致grandfather的平衡因子变为-2，平衡树失衡，所以需要利用旋转来降低高度！

• 首先以subL为轴，将subLR向上提（左旋），将grandfather、parent和subL旋转至一条直线上；
• 再以parent为轴将之前的subLR向上提（右旋），左树的高度降1，grandfather的平衡因子加1后变为-1，恢复平衡状态。
• 双旋完成后将parent、subL的平衡因子置为0即可，左右双旋也就完成啦！

2. parent有两个孩子：没有插入subRL或subRR之前的AVL树一定是处于平衡状态的，并且满足AVL树的性质。

　　正是由于插入了节点subRL或者subRR，导致其祖先节点的平衡因子被改变，grandfather的平衡因子变为-2，平衡态比打破，需要进行旋转来降低高度！

• 首先parent为轴将subR节点往上提至原parent的位置（左旋），将grandfather、parent 和 subR旋至一条直线上；
• 再以grandfather为轴将subR往上提至grandfather的位置（右旋），此时以subR为根的左右子树的高度相同，恢复了平衡态！

parent有两个孩子时，要看插入的节点是subR的右孩子还是左孩子，双旋后对平衡因子的修改分两种情况：

• subR的平衡因子为1，即subR有右孩子无左孩子（有subRR但无subRL），双旋之后将grandfather的平衡因子置为0，将parent的平衡因子置为-1；
• subR的平衡因子为-1，即subR有左孩子无右孩子（有subRL但无subRR），双旋之后将grandfather的平衡因子置为1，将parent的平衡因子置为0；

//左右双旋
template<class K, class V>
void AVLTree<K, V>::_RotateLR(AVLTreeNode<K, V>*&  parent)
{
	AVLTreeNode<K, V>* pNode = parent;
	AVLTreeNode<K, V>* subL = parent->_left;
	AVLTreeNode<K, V>* subLR = subL->_right;
	int bf = subLR->_bf;

	_RotateL(parent->_left);
	_RotateR(parent);

	if (bf == 1)
	{
		pNode->_bf = 0;
		subL->_bf = -1;
	}
	else if (bf == -1)
	{
		pNode->_bf = 1;
		subL->_bf = 0;
	}
	else
	{
		pNode->_bf = 0;
		subL->_bf = 0;
	}

}

　

---

　右左双旋：

1. parent只有一个孩子：由于节点subRL的插入破坏了AVL树的平衡，parent的平衡因子变为2，需要利用旋转来降低高度！

• 首先，以subR为轴，将subRL提上去（右旋），保证parent、subR 和 subRL在一条直线上；
• 以parent为轴，将上一步标记为subRL的节点向上升（左旋），这样达到了降低高度的目的；
• 双旋之后，parent和subR的平衡因子都要置为0

2.parent有两个孩子：没有插入subLL或者subLR之前的AVL树一定是处于平衡状态的，并且满足AVL树的性质。

　　正是由于插入了节点subLL或者subLR，导致其祖先节点的平衡因子被改变，grandfather的平衡因子变为2，平衡态比打破，需要进行旋转来降低高度！

• 首先parent为轴将subL节点往上提至原parent的位置（右旋），将grandfather、parent 和 subL旋至一条直线上；
• 再以grandfather为轴将subL往上提至grandfather的位置（左旋），此时以subL为根的左右子树的高度相同，恢复了平衡态！

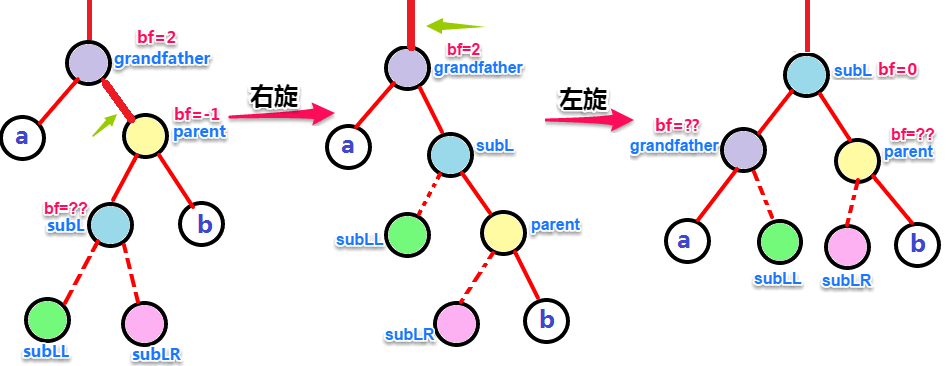
parent有两个孩子时，要看插入的节点是subL的右孩子还是左孩子，双旋后对平衡因子的修改分两种情况：

• subL的平衡因子为1，即subL有右孩子无左孩子（有subLR但无subLL），双旋之后将grandfather的平衡因子置为-1，将parent的平衡因子置为0；
• subL的平衡因子为-1，即subL有左孩子无右孩子（有subLL但无subLR），双旋之后将grandfather的平衡因子置为0，将parent的平衡因子置为1；　

//右左双旋
template<class K, class V>
void AVLTree<K, V>::_RotateRL(AVLTreeNode<K, V>*&  parent)
{
	AVLTreeNode<K, V>* pNode = parent;
	AVLTreeNode<K, V>* subR= parent->_right;
	AVLTreeNode<K, V>* subRL = subR->_left;
	int bf = subRL->_bf;

	_RotateR(parent->_right);
	_RotateL(parent);

	if (bf == 1)
	{
		pNode->_bf = 0;
		subR->_bf = -1;
	}
	else if (bf == -1)
	{
		pNode->_bf = 1;
		subR->_bf = 0;
	}
	else
	{
		pNode->_bf = 0;
		subR->_bf = 0;
	}
}