BZOJ 小Z的袜子 2038 国家集训队

过程：

想了很久如何求组合数C（n，m），然而 YL 同学提醒了可以直接除以 2*n*（n - 1 ）。改了之后果然对了，以为一定是一次性AC 了，然而 WA 了3次，尴尬 ——

神 TM，ZC 苟看了题解说要开 long long，幡然醒悟会 int 爆炸 。

暴力：

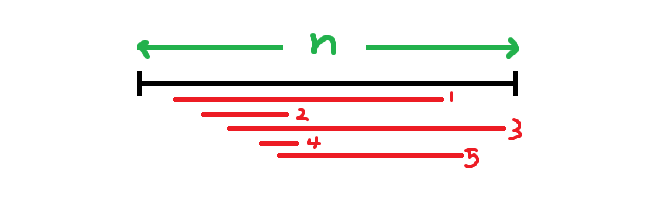
很容易想到，可以将区间排序，第一关键字为左区间越小越好，第二关键字为右区间端点越大越好 。

然而这样做看起来复杂度很可观，因为最坏情况是O（nq）的：

想暴力跳吗？

那么你会来回跳的，TLE 。

正解：

回到排序的问题，我们是将左右定为关键字的，然而这样不能保证有区间是单调递增的，也就是会出现反复横跳的情况 。

那么我们如何保证反复横跳不出现，或者少出现，或者横跳的范围尽量小呢？

不错，就是莫队算法 。

莫队算法就是一个强大的暴力 。

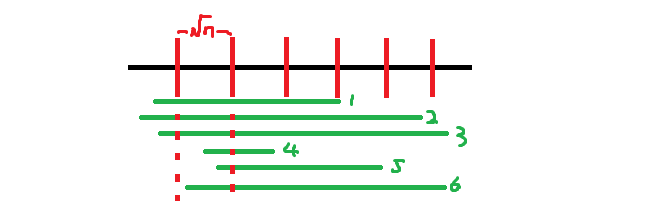
我们其实只需要调整一下排序关键字就好了，首先将整个袜子序列分成 Sqrt（n）个块（分块算法），并将属于同一个块的所有区间按照右区间端点越大越好；不属于同一个块的所有区间按照左区间端点越小越好 。

嘿，为什么这样是正确的呢？

这样只需要暴力反复横跳左区间端点，而对于左区间对应的每一个块的右区间一个一个跳是O（n）的，像刷子一样，而这样右区间端点绝对不会走回头路！

所有块的横跳复杂度是 q * Sqrt（n），右端点的指针最多每一个块 For n 次；

所以最终的复杂度是O（（n + q）* Sqrt（n））！

现在你已经解决了本题的大 Boss 了！

但时间复杂度解决了，如何统计答案呢（小 Boss）？

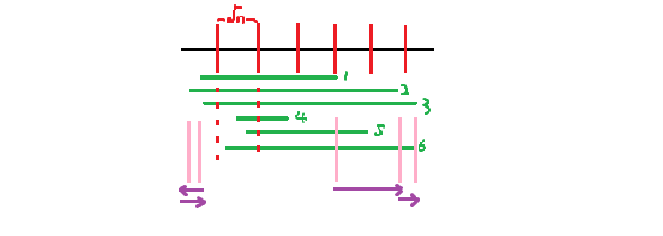
小区间对大区间是有贡献的，所以可以用小区间去更新大区间 。

情况1：

如果小区间的左端点 > 大区间的左端点，那么说明 大区间在小区间 左端点左边 的某一部分没有包含，说明需要将这一段统计。

情况2：

如果小区间的左端点 < 大区间的左端点，那么说明 小区间在大区间 左端点左边 的某一部分统计多了，说明需要将这一段删除贡献 。

如何统计答案？

对于每加进一个新的结点，它对已经加入的结点都有 1 的贡献；所以如何知道已经加入多少个点了呢？

假设加入的是第 i 只袜子 。可以开桶记录已经统计了 Bucket [ C [ i ] ] 个同 C [ i ] 颜色相同的袜子，现在，加入一个颜色为 C [ i ] 的袜子，那么贡献就是 Bucket [ C [ i ] ]！

对于每加退出一个旧的结点，它原本对已经加入的结点都有 Bucket [ C [ i ] ] - 1 的贡献；原本贡献是Bucket [ C [ i ] ] - 1 的原因是它加入的时候有 Bucket [ C [ i ] ] - 1 只同色袜子被统计，那么退群的时候就只需要减去它加入时的贡献就好了！

没有完，区间分布可能有很多个块，所以需要跳块 。

有两个选择，第一个是暴力跳块，就是和跳左右区间一样的道理，需要维护入桶和出桶；另一个是直接到下一个块的第一个左端点直接开始处理，这之前只需要将 Bucket 数组清零就行，不会 T，因为最多清零 Sqrt（n）次，每次复杂度为 O（50000），炸不了 。

输出处理答案需要注意是最简分数，同时除以 Gcd 就好了啊，用一个结构体 ansx 保存一下分子和分母就好了 。

注意区间是排好序的（打乱了），所以必须记录 id，表示当前处理的区间的前身是 id 号区间，将分子分母存入ansx [ id ] 。

 /**************************************************************
     Problem: 2038
     User: jerrywans
     Language: C++
     Result: Accepted
     Time:728 ms
     Memory:4432 kb
 ****************************************************************/  

 #include <bits/stdc++.h>  

 const  int  N =  +  ;  

 int  a [ N ] , pos [ N ] , bucket [ N ] ;
 int  n , m , block ;
 long  long  ans ;  

 struct  Node {
     int  l , r , id ;
     short  operator  < ( const  Node  &  rhs )  const  {
         if ( pos [ l ] == pos [ rhs . l ] )  return  r < rhs . r ; // 关键字排序
         return  l < rhs . l ;
     }
 }
 grid [ N ] ;  

 struct  Ans {
     int  fst , sec ; // fst是分子，sec是分母
 }
 ansx [ N ] ;  

 int  gcd ( long long  a , long long  b ) {
     return  b ==  ? a : gcd ( b , a % b ) ;
 }  

 int  modify ( long long  x , long long  y , int  id ) {
     int  d = gcd ( x , y ) ;
     if ( x ==  )  ansx [ id ] . fst =  , ansx [ id ] . sec =  ;
     else  ansx [ id ] . fst = x / d , ansx [ id ] . sec = y / d ;
 }  

 void  work ( ) {
     int  lasl = grid [  ] . l , lasr = grid [  ] . r ;
     for ( int  i = lasl ; i <= lasr ; i ++ ) {
         ans += 1ll * bucket [ a [ i ] ] ;
         bucket [ a [ i ] ] ++ ;
     }
     modify ( ans , 1ll * ( lasr - lasl +  ) * ( lasr - lasl ) /  , grid [  ] . id ) ;
     for ( int  q =  ; q <= m ; q ++ ) {
         int  nowl = grid [ q ] . l , nowr = grid [ q ] . r ;
         if ( pos [ nowl ] == pos [ lasl ] ) {
             if ( nowl < lasl ) {
                 for ( int  i = nowl ; i < lasl ; i ++ ) {
                     ans += 1ll * bucket [ a [ i ] ] ;
                     bucket [ a [ i ] ] ++ ;
                 }
             }
             if ( nowl > lasl ) {
                 for ( int  i = lasl ; i < nowl ; i ++ ) {
                     bucket [ a [ i ] ] -- ;
                     ans -= 1ll * bucket [ a [ i ] ] ;
                 }
             }
             for ( int  i = lasr +  ; i <= nowr ; i ++ ) {
                 ans += 1ll * bucket [ a [ i ] ] ;
                 bucket [ a [ i ] ] ++ ;
             }
             modify ( ans , 1ll * ( nowr - nowl +  ) * ( nowr - nowl ) /  , grid [ q ] . id ) ;
             lasl = nowl , lasr = nowr ;
         }
         else {
             ans =  ;
             lasl = nowl , lasr = nowr ;
             memset ( bucket ,  , sizeof ( bucket ) ) ;
             for ( int  i = nowl ; i <= nowr ; i ++ ) {
                 ans += 1ll * bucket [ a [ i ] ] ;
                 bucket [ a [ i ] ] ++ ;
             }
             modify ( ans , 1ll * ( nowr - nowl +  ) * ( nowr - nowl ) /  , grid [ q ] . id ) ;
         }
     }
 }  

 int  main ( ) { // 离线，莫队  

     scanf ( "%d%d" , & n , & m ) ;
     block = ( int ) sqrt ( n ) ;
     for ( int  i =  ; i <= n ; i ++ )  scanf ( "%d" , & a [ i ] ) ;
     for ( int  i =  ; i <= m ; i ++ ) {
         scanf ( "%d%d" , & grid [ i ] . l , & grid [ i ] . r ) ;
         grid [ i ] . id = i ;
     }
     for ( int  i =  ; i <= n ; i ++ )  pos [ i ] = ( i -  ) / block +  ; // 记录每个结点属于的块的编号
     std :: sort ( grid +  , grid + m +  ) ;
     work ( ) ;
     for ( int  i =  ; i <= m ; i ++ )
         printf ( "%d/%d\n" , ansx [ i ] . fst , ansx [ i ] . sec ) ; // 按照区间顺序输出解  

     return   ;
 }
 /*
 6 4
 1 2 3 3 3 2
 2 6
 1 3
 3 5
 1 6
 */  

Ans