poj1177 Picture 矩形周长并

地址：http://poj.org/problem?id=1177

题目：

Picture

Time Limit: 2000MS		Memory Limit: 10000K
Total Submissions: 12905		Accepted: 6817

Description

A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.

Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.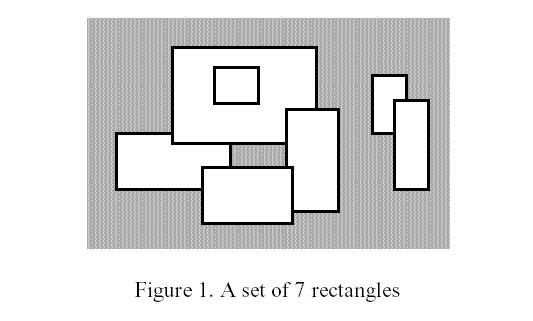 

The corresponding boundary is the whole set of line segments drawn in Figure 2.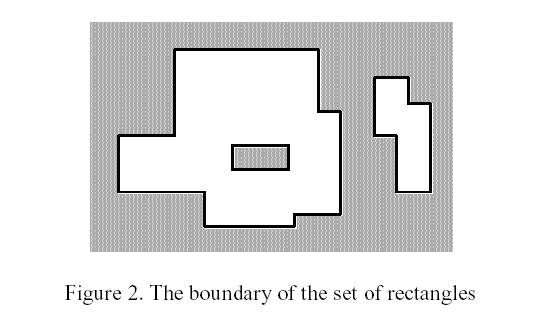 

The vertices of all rectangles have integer coordinates. 

Input

Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.

0 <= number of rectangles < 5000 
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.

Output

Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.

Sample Input

7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16

Sample Output

228

Source

IOI 1998

 

思路：

　　复习下。。。

　

 #include <cstdio>
 #include <algorithm>
 #include <cstring>
 #include <cmath>

 using namespace std;

 #define MP make_pair
 #define PB push_back
 #define lc (o<<1)
 #define rc (o<<1|1)
 typedef long long LL;
 typedef pair<int,int> PII;
 const double eps=1e-;
 const double pi=acos(-1.0);
 const int K=5e3+;
 const int mod=1e9+;

 struct node
 {
     int l,r,y,f;
     bool operator < (const node &ta)const
     {
         return y<ta.y;
     }
 }seg[K*];
 int cover[K*],sum[K*],lp[K*],rp[K*],cnt[K*];
 int hs[K*];
 void push_up(int o,int l,int r)
 {
     if(cover[o])
         sum[o]=hs[r+]-hs[l],lp[o]=rp[o]=cnt[o]=;
     else if(l==r)
         sum[o]=lp[o]=rp[o]=cnt[o]=;
     else
     {
         sum[o]=sum[lc]+sum[rc];
         lp[o]=lp[lc],rp[o]=rp[rc];
         cnt[o]=cnt[lc]+cnt[rc]-(rp[lc]&lp[rc]);
     }
 }
 void update(int o,int l,int r,int nl,int nr,int f)
 {
     if(l==nl&&r==nr)
         cover[o]+=f,push_up(o,l,r);
     else
     {
         int mid=l+r>>;
         if(nr<=mid) update(lc,l,mid,nl,nr,f);
         else if(nl>mid) update(rc,mid+,r,nl,nr,f);
         else    update(lc,l,mid,nl,mid,f),update(rc,mid+,r,mid+,nr,f);
         push_up(o,l,r);
     }
 }
 int main(void)
 {
     int n;
     while(~scanf("%d",&n)&&n)
     {
         int tot=,ans=;
         memset(cover,,sizeof cover);
         memset(lp,,sizeof lp);
         memset(rp,,sizeof rp);
         memset(cnt,,sizeof cnt);
         memset(sum,,sizeof sum);
         for(int i=,lx,ly,rx,ry;i<=n;i++)
         {
             scanf("%d%d%d%d",&lx,&ly,&rx,&ry);
             seg[tot+]=(node){lx,rx,ly,};
             seg[tot+]=(node){lx,rx,ry,-};
             hs[tot+]=lx,hs[tot+]=rx;
             tot+=;
         }
         sort(seg+,seg++tot);
         sort(hs+,hs++tot);
         int sz=unique(hs+,hs++tot)-hs,ls=;
         for(int i=;i<=tot;i++)
         {
             int l=lower_bound(hs+,hs+sz,seg[i].l)-hs;
             int r=lower_bound(hs+,hs+sz,seg[i].r)-hs;
             update(,,sz,l,r-,seg[i].f);
             ans+=abs(ls-sum[]);
             if(i!=tot)
                 ans+=*cnt[]*(seg[i+].y-seg[i].y);
             ls=sum[];
         }
         printf("%d\n",ans);
     }
     return ;
 }