对数损失函数(Logarithmic Loss Function)的原理和 Python 实现

原理

　　对数损失, 即对数似然损失(Log-likelihood Loss), 也称逻辑斯谛回归损失(Logistic Loss)或交叉熵损失(cross-entropy Loss), 是在概率估计上定义的.它常用于(multi-nominal, 多项)逻辑斯谛回归和神经网络,以及一些期望极大算法的变体. 可用于评估分类器的概率输出.

　　对数损失通过惩罚错误的分类,实现对分类器的准确度(Accuracy)的量化. 最小化对数损失基本等价于最大化分类器的准确度.为了计算对数损失, 分类器必须提供对输入的所属的每个类别的概率值, 不只是最可能的类别. 对数损失函数的计算公式如下:

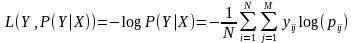
　　其中, Y 为输出变量, X为输入变量, L 为损失函数. N为输入样本量, M为可能的类别数, y_ij是一个二值指标, 表示类别 j 是否是输入实例 x_i的真实类别. p_ij 为模型或分类器预测输入实例 x_i 属于类别 j 的概率.

　　如果只有两类 {0, 1}, 则对数损失函数的公式简化为

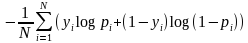
　　这时, y_i 为输入实例 x_i 的真实类别, p_i 为预测输入实例 x_i 属于类别 1 的概率. 对所有样本的对数损失表示对每个样本的对数损失的平均值, 对于完美的分类器, 对数损失为 0 .

Python 实现

采用自定义 logloss 函数和 scikit-learn 库中 sklearn.metrics.log_loss 函数两种方式实现对数损失, 如下所示:

#!/usr/bin/env python

# -*- coding: utf8 -*-

#author: klchang

#date: 2018.6.23

# y_true: list, the true labels of input instances

# y_pred: list, the probability when the predicted label of input instances equals to 1

def logloss(y_true, y_pred, eps=1e-15):

    import numpy as np

    # Prepare numpy array data

    y_true = np.array(y_true)

    y_pred = np.array(y_pred)

    assert (len(y_true) and len(y_true) == len(y_pred))

    # Clip y_pred between eps and 1-eps

    p = np.clip(y_pred, eps, 1-eps)

    loss = np.sum(- y_true * np.log(p) - (1 - y_true) * np.log(1-p))

    return loss / len(y_true)

def unitest():

    y_true = [0, 0, 1, 1]

    y_pred = [0.1, 0.2, 0.7, 0.99]

    print ("Use self-defined logloss() in binary classification, the result is {}".format(logloss(y_true, y_pred)))

    from sklearn.metrics import log_loss

    print ("Use log_loss() in scikit-learn, the result is {} ".format(log_loss(y_true, y_pred)))

if __name__ == '__main__':

    unitest()

注: 在实现时, 加入参数 eps, 避免因预测概率输出为 0 或 1 而导致的计算错误的情况; 对数损失函数的输入参数 y_pred 为当预测实例属于类 1 时的概率; 对数损失采用自然对数计算结果.

参考资料

1. Log Loss. http://wiki.fast.ai/index.php/Log_Loss

2. Making Sense of Logarithmic Loss. https://www.r-bloggers.com/making-sense-of-logarithmic-loss/

3. What is an intuitive explanation for the log loss function. https://www.quora.com/What-is-an-intuitive-explanation-for-the-log-loss-function

4. log-loss in scikit-learn documentation. http://scikit-learn.org/stable/modules/model_evaluation.html#log-loss

5. sklearn documentation-sklearn.metrics.log_loss. http://scikit-learn.org/stable/modules/generated/sklearn.metrics.log_loss.html#sklearn.metrics.log_loss

6. 李航. 统计学习方法. 北京: 清华大学出版社. 2012