百度2017笔试题：寻找n个员工中未打卡的那一个

声明：图片来自网络，笔者只是试着做了一下，然后做个记录。

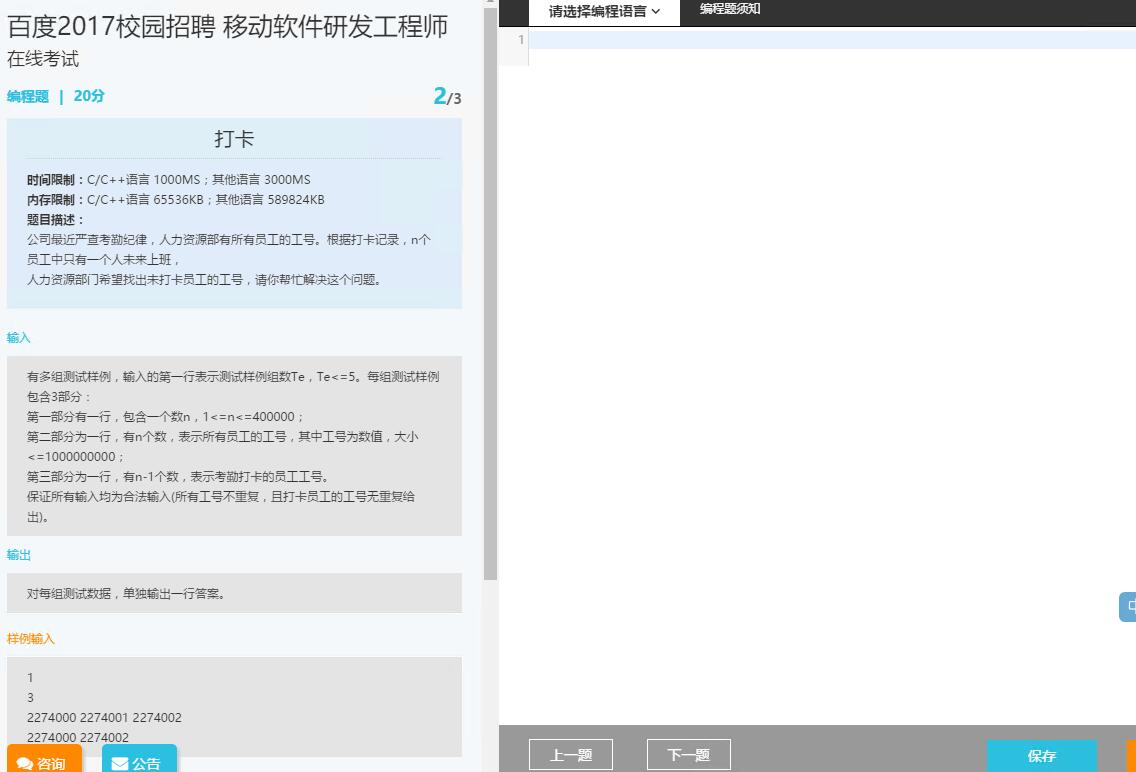
拿到这个题目的时候，笔者首先想到的是二分。两个数组，一个是全体员工的集合A；一个是缺少一人的集合B。对A,B排序，再对B进行二分，得到B的中间员工的工号mid，若A[mid] == B[mid]，那么缺席员工的工号在mid之后，继续二分；若A[mid] < B[mid]，那么缺席员工的工号在mid之前，继续二分。值得注意的是，这里A[mid]是不会大于B[mid]的。另外，这里的二分仅针对缺席工号在数组中间的情况。若缺席工号在数组(当然是排序后)首尾，单独处理即可。

 #include <bits/stdc++.h>
 using namespace std;

 typedef long long LL;
 #define MOD        1000000007ll
 #define PI         acos(-1.0)
 const double EPS = 1e-;
 //const double PI  = acos(-1.0);
 const int INF = 0x3f3f3f3f;
 //const LL  MOD = 1e9+7;

 template <class T> inline T bigMod(T p, T e, T M){
     long long ret = ;
     for(; e > ; e >>= ){
         if(e & ) ret = (ret * p) % M;
         p = (p * p) % M;
     } return (T)ret % M;    // Attention: bigMod(p, 0, 1), so ret has to module M.
 }
 template <class T> inline T modInverse(T a, T M){return bigMod(a, M-, M);}
 template <class T> inline T gcd(T a, T b){return b ? gcd(b, a%b) : a;}
 int main() {
     int T;
     scanf("%d", &T);
     for (int i = ; i <= T; ++i) {
         vector<int> total;
         vector<int> arrive;
         int num; cin >> num;
         for (int j = ; j < num; ++j) {
             int employee; cin >> employee;
             total.push_back(employee);
         }
         for (int j = ; j < num - ; ++j) {
             int arriver; cin >> arriver;
             arrive.push_back(arriver);
         }
         /***     binary search
         sort(total.begin(), total.end());
         sort(arrive.begin(), arrive.end());
         if (total[0] != arrive[0]) cout << total[0] << endl;
         else if (total[num-1] != arrive[num-2]) cout << total[num-1] << endl;
         else {
             int left = 0, right = num - 2;
             while(left <= right) {
                 int mid = left + (right - left)/2;
                 if (total[mid] == arrive[mid]) {
                     left = mid + 1;
                 }else if (total[mid] < arrive[mid]){
                     right = mid - 1;
                 }
             }
             cout << total[left] << endl;
         }*/
         int num1 = ;
         for (auto iter = total.begin(); iter != total.end(); ++iter) {
             num1 = num1 ^ *iter;
         }
         int num2 = ;
         for (auto iter = arrive.begin(); iter != arrive.end(); ++iter) {
             num2 = num2 ^ *iter;
         }
         cout << (num1 ^ num2) << endl;
     }
     return ;
 }

后来有个朋友提出了一个更好的方法，简直漂亮。利用异或的思想。

我们先来看这样一个表达式： p ^ q = m, m等于p,q的异或。那么有，p = q ^ m,  q = p ^ m。

现在，回过头来看这个题目。我们把A中的元素互相异或得到m；把B中的元素互相异或得到p。那么，没来的哪个员工工号是q=m^p。

代码的实现也综合在上诉代码中。