HDU 3988 Harry Potter and the Hide Story（数论-整数和素数）

Harry Potter and the Hide Story

Problem Description

iSea is tired of writing the story of Harry Potter, so, lucky you, solving the following problem is enough.

 

Input

The first line contains a single integer T, indicating the number of test cases.

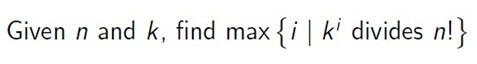
Each test case contains two integers, N and K. 



Technical Specification



1. 1 <= T <= 500

2. 1 <= K <= 1 000 000 000 000 00

3. 1 <= N <= 1 000 000 000 000 000 000

 

Output

For each test case, output the case number first, then the answer, if the answer is bigger than 9 223 372 036 854 775 807, output “inf” (without quote).

 

Sample Input

2
2 2
10 10

 

Sample Output

Case 1: 1
Case 2: 2

 

Author

iSea@WHU

 

Source

field=problem&key=2011%20Multi-University%20Training%20Contest%2015%20-%20Host%20by%20WHU&source=1&searchmode=source" style="color:rgb(26,92,200); text-decoration:none">2011 Multi-University Training
Contest 15 - Host by WHU

 

Recommend

lcy   |   We have carefully selected several similar problems for you:  3987 3986 

pid=3983" target="_blank" style="color:rgb(26,92,200); text-decoration:none">3983 

pid=3984" target="_blank" style="color:rgb(26,92,200); text-decoration:none">3984 3985 

 

题目大意：

给定 n和k ， 求 n! % k^i 等于0时，i 的最大取值是多少？

解题思路：

将 k分解质因素。n也依据k的质因素求出关系限制i，最后算出最大的i就可以。

解题代码：

#include <iostream>
#include <cstdio>
#include <map>
#include <vector>
#include <cstring>
using namespace std;

typedef unsigned long long ll;
ll n,k;

const int maxn=10000010;
bool isPrime[maxn];
vector <ll> v;
ll tol;

void get_prime(){
    tol=0;
    memset(isPrime,true,sizeof(isPrime));
    for(ll i=2;i<maxn;i++){
        if(isPrime[i]){
            tol++;
            v.push_back(i);
        }
        for(ll j=0;j<tol && i*v[j]<maxn;j++){
            isPrime[i*v[j]]=false;
            if(i%v[j]==0) break;
        }
    }
    //for(ll i=v.size()-1;i>=v.size()-100;i--) cout<<v[i]<<endl;
}

map <ll,ll> getPrime(ll x){
    map <ll,ll> mp;
    for(ll i=0;i<tol && x>=v[i];i++){
        while(x>0 && x%v[i]==0){
            x/=v[i];
            mp[v[i]]++;
        }
    }
    if(x>1) mp[x]++;
    return mp;
}

void solve(){
    if(k==1){
        printf("inf\n");
        return;
    }
    map <ll,ll> mp=getPrime(k);
    ll ans=1e19;
    for(map <ll,ll>::iterator it=mp.begin();it!=mp.end();it++){
        ll tmp=n,sum=0;
        while(tmp>0){
            sum+=tmp/(it->first);
            tmp/=(it->first);
        }
        if(sum/(it->second)<ans) ans=sum/(it->second);
    }
    cout<<ans<<endl;
}

int main(){
    get_prime();
    int t;
    scanf("%d",&t);
    for(int i=0;i<t;i++){
        cin>>n>>k;
        printf("Case %d: ",i+1);
        solve();
    }
    return 0;
}

版权声明：本文博客原创文章。博客，未经同意，不得转载。