P6100 [USACO19FEB]Painting the Barn G

本题解提供的做法思路应该是比较清晰的，可惜代码实现比较繁琐，仅供大家参考。

题解

不难发现 \(x\) ，\(y\) 的取值范围只有 \(200\) ，所以我们可以考虑从这里入手。我们可以先通过二维前缀和将每个点的上色次数算出来，然后考虑再画矩形。

我们可以先考虑一个矩形的情况，不难发现，如果矩形内的每有一个 \(k-1\) 可以使答案加一，每有一个 \(k\) 可以使答案减一。那如果我们要使答案最大，肯定是 \(1\) 与 \(-1\) 的最大的一个矩阵，发现就是做一个最大矩阵和，可以 \(O(200^3)\) 去搞。

我们再来考虑两个矩形的情况，不难发现，如果是两个边与 \(x\) 轴和 \(y\) 轴平行的不相交的矩形，我们肯定可以用一条平行与 \(x\) 轴或 \(y\) 轴的直线将其分开。如图：

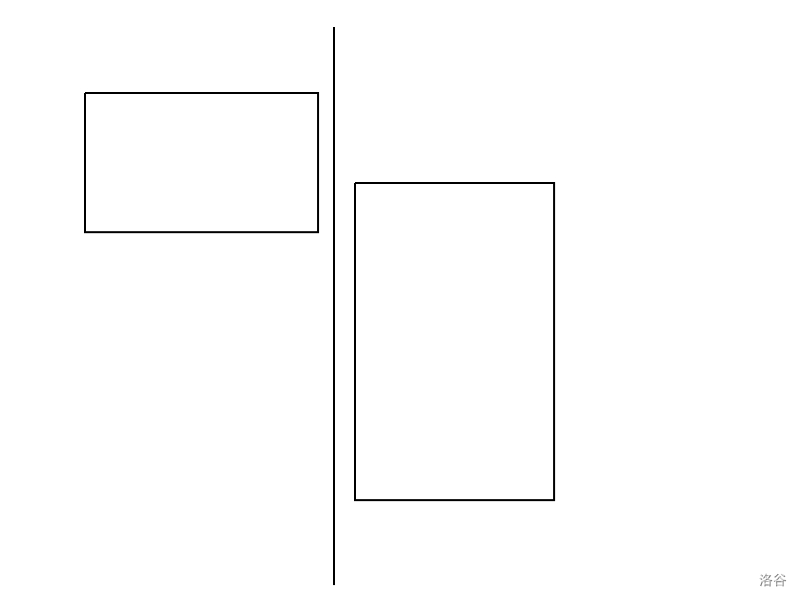
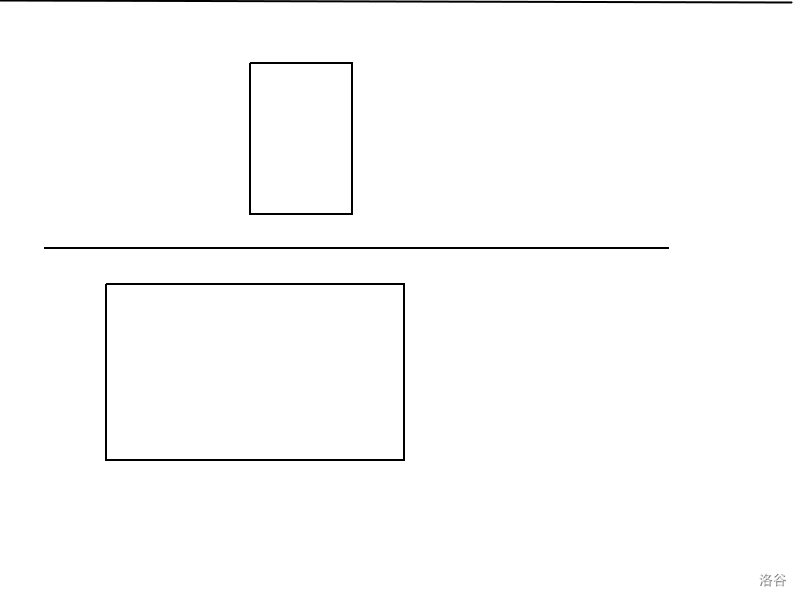
所以我们只需要将整个平面通过平行于 \(x\) 轴和 \(y\) 轴的直线分成两部分，再在其中做最大矩阵和就可以了。

当然直接做是肯定会炸的，所以你需要进行一堆的预处理和前缀和，仔细一点就好了。

以上。

代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,M=205,K=1e5+5;
int n,m=200,k;
int h[M][M],res=0,ans=0;
int cntx[M][M],cnty[M][M];
int ansx[M][M],ansy[M][M];
int hhhx[2][M],hhhy[2][M];
int main()
{
	cin>>n>>k;
	for(int i=1,x1,y1,x2,y2;i<=n;++i)
	{
		scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
		++x1,++y1,++x2,++y2;
		h[x1][y1]++,h[x2][y2]++;
		h[x1][y2]--,h[x2][y1]--;
	}
	for(int i=1;i<=m;++i)
	{
		for(int j=1;j<=m;++j)
		h[i][j]+=h[i-1][j]+h[i][j-1]-h[i-1][j-1],res+=(h[i][j]==k);
	}
	// for(int i=1;i<=8;++i)
	// {
	// 	for(int j=1;j<=8;++j)
	// 	printf("%d ",h[i][j]);
	// 	printf("\n");
	// }
	// printf("\n");
	for(int i=1;i<=m;++i)
	{
		for(int j=1;j<=m;++j)
		{
			cntx[i][j]=cntx[i-1][j]+(h[i][j]==k-1)-(h[i][j]==k);
			cnty[i][j]=cnty[i][j-1]+(h[i][j]==k-1)-(h[i][j]==k);
		}
	}
	// for(int i=1;i<=8;++i)
	// {
	// 	for(int j=1;j<=8;++j)
	// 	printf("%d ",cntx[i][j]);
	// 	printf("\n");
	// }
	// printf("\n");
	// for(int i=1;i<=8;++i)
	// {
	// 	for(int j=1;j<=8;++j)
	// 	printf("%d ",cnty[i][j]);
	// 	printf("\n");
	// }
	// printf("\n");
	int tmp;
	for(int i=1;i<=m;++i)
	{
		for(int j=1;j<=i;++j)
		{
			tmp=0;
			for(int c=1;c<=m;++c)
			{
				tmp=max(tmp+cntx[i][c]-cntx[j-1][c],0);
				ansx[i][j]=max(ansx[i][j],tmp);
			}
		}
	}
	for(int i=1;i<=m;++i)
	{
		for(int j=1;j<=i;++j)
		{
			tmp=0;
			for(int c=1;c<=m;++c)
			{
				tmp=max(tmp+cnty[c][i]-cnty[c][j-1],0);
				ansy[i][j]=max(ansy[i][j],tmp);
			}
		}
	}
	// for(int i=1;i<=8;++i)
	// {
	// 	for(int j=1;j<=8;++j)
	// 	printf("%d ",ansx[i][j]);
	// 	printf("\n");
	// }
	// printf("\n");
	// for(int i=1;i<=8;++i)
	// {
	// 	for(int j=1;j<=8;++j)
	// 	printf("%d ",ansy[i][j]);
	// 	printf("\n");
	// }
	// printf("\n");
	for(int i=1;i<=m;++i)
	{
		hhhx[0][i]=hhhx[0][i-1];
		for(int j=1;j<=i;++j)
		hhhx[0][i]=max(hhhx[0][i],ansx[i][j]);
	}
	for(int i=m;i>=1;--i)
	{
		hhhx[1][i]=hhhx[1][i+1];
		for(int j=m;j>=i;--j)
		hhhx[1][i]=max(hhhx[1][i],ansx[j][i]);
	}
	for(int i=1;i<=m;++i)
	{
		hhhy[0][i]=hhhy[0][i-1];
		for(int j=1;j<=i;++j)
		hhhy[0][i]=max(hhhy[0][i],ansy[i][j]);
	}
	for(int i=m;i>=1;--i)
	{
		hhhy[1][i]=hhhy[1][i+1];
		for(int j=m;j>=i;--j)
		hhhy[1][i]=max(hhhy[1][i],ansy[j][i]);
	}
	ans=res;
	for(int i=2;i<=m;++i) ans=max(ans,res+hhhx[0][i-1]+hhhx[1][i]);
	for(int i=2;i<=m;++i) ans=max(ans,res+hhhy[0][i-1]+hhhy[1][i]);
	printf("%d\n",ans);
	return 0;
}