POJ2484 A Funny Game[博弈论]

A Funny Game

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 5401		Accepted: 3381

Description

Alice and Bob decide to play a funny game. At the beginning of the game they pick n(1 <= n <= 10⁶) coins in a circle, as Figure 1 shows. A move consists in removing one or two adjacent coins, leaving all other coins untouched. At least one coin must be removed. Players alternate moves with Alice starting. The player that removes the last coin wins. (The last player to move wins. If you can't move, you lose.) 
 
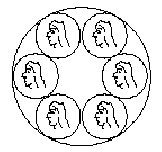
Figure 1
Note: For n > 3, we use c1, c2, ..., cn to denote the coins clockwise and if Alice remove c2, then c1 and c3 are NOT adjacent! (Because there is an empty place between c1 and c3.)

Suppose that both Alice and Bob do their best in the game. 
You are to write a program to determine who will finally win the game. 

Input

There are several test cases. Each test case has only one line, which contains a positive integer n (1 <= n <= 10⁶). There are no blank lines between cases. A line with a single 0 terminates the input. 

Output

For each test case, if Alice win the game,output "Alice", otherwise output "Bob". 

Sample Input

1
2
3
0

Sample Output

Alice
Alice
Bob

Source

POJ Contest,Author:Mathematica@ZSU

---

题意：环，取1或2个相邻的

---

Alice取完后变成链了，可以先递推链的(利用N和P的关系)

发现全是N状态

所以只有1 2时Alice，否则Bob

 

题解是这么分析的：

典型的对称博弈。当n>=3时，无论A如何选择，B选择一个特殊的位置（1个或者连续2个）正好把剩下的环路分成两个链路，大小相同。接下来，无论A选择两个链路中哪一个，进行何种操作，B只需要选择另一个链路中，进行相同的操作。剩下的系统，仍是对称的。直到最后，B肯定是最后一个进行操作的。

#include <cstdio>
inline int read(){
    char c=getchar();int x=,f=;
    while(c<''||c>''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x*f;
}
int n;
int main(int argc, const char * argv[]) {
    while((n=read())){
        if(n>=) puts("Bob");
        else puts("Alice");
    }
    return ;
}