【新阁教育】穷学上位机系列——搭建STEP7仿真环境

经常有学员问我，学习上位机要不要买PLC硬件？

我一般的回答是：富则自行购买，穷则搭建仿真。

PLC硬件，对于学习上位机来说，是锦上添花的事，经济条件允许，有则更好，条件不允许，我们也可以通过搭建仿真环境的方式来学习，因此我专门准备了一个系列——穷学上位机系列。

01、写在前面

本文的主题是基于STEP7搭建西门子仿真环境，STEP7是西门子300系列、400系列的编程软件，早期学习PLC的小伙伴对这个一定不陌生，虽然现在可以在TIA环境下编写S7-300/400的程序，但是不可否认，仍然有很多企业（尤其是制造业）在使用S7-300/400 PLC，如果仅仅使用S7-300/400，我觉得STEP7相比博图来说，会更加小巧和方便。
软件环境：SIMATIC Manager V5.6、PLCSIM V5.4、NetToPLCsim、CMSPro硬件环境：WIN10 64位

软件获取关键词：STEP7、PLCSIM、NetToPLCsim、CMSPro【dotNet工控上位机：thinger_swj】

02、仿真步骤

1、创建项目：使用STEP7创建一个PLC项目，取名thinger_cn_PLCSimulator，插入一个SIMATIC 300站点，如下所示：

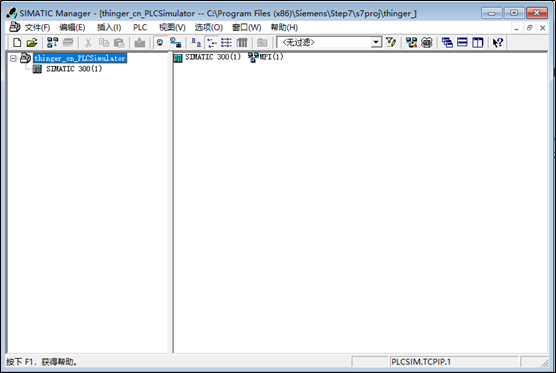
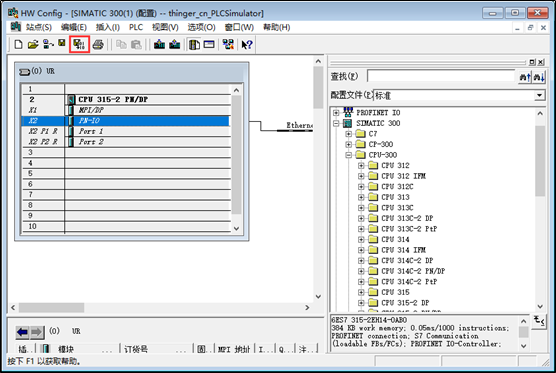
2、硬件组态：打开硬件组态，首先插入一个机架Rack，然后插入一个S7-300的CPU，最好直接选择带PN接口的，这里选择的是CPU 315-2 PN/DP，如下所示：

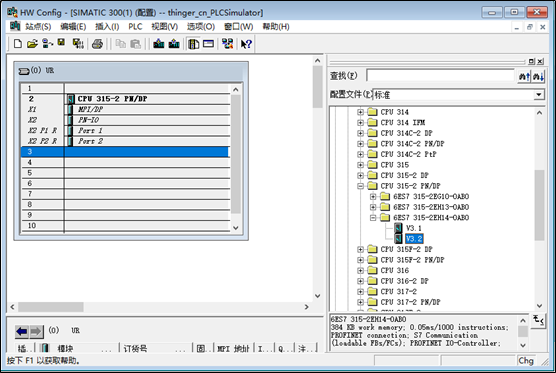
3、创建Ethernet：双击上图中的PN-IO，在弹出的窗体中，选择属性>>新建，然后将IP地址修改成192.168.1.123，这里的IP地址是自己设置的，只要和本机在同一网段即可。

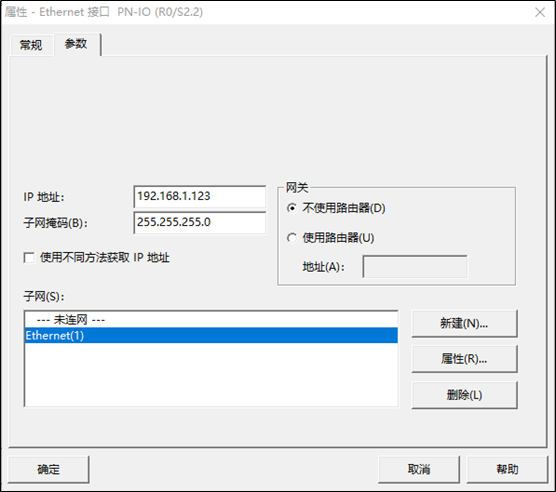
4、编译保存：点击下图中的红框图标，将硬件组态编译并保存。件仿真300/400PLC，而不需要安装庞大的博图软件，而且这里主要采用的是NetToPLCsim的方案，也不需要安装PLCSIM-Advanced。

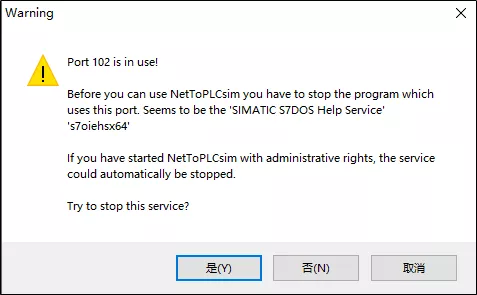
5、启动NetToPLCsim：以管理员权限运行NetToPLCsim，会弹出以下窗口，选择是即可。

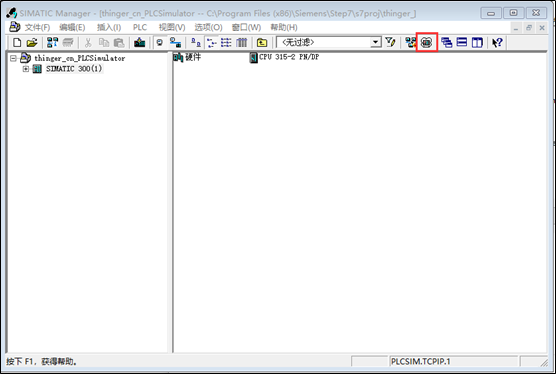
6、启动PLCSIM：在SIMATIC Manager窗体中，点击下图中的红框图标，启动PLCSIM，如果该图标为灰色，说明PLCSIM未安装。

7、下载PLC程序：在SIMATIC Manager窗体中，点击下图中的红框图标，下载PLC程序。

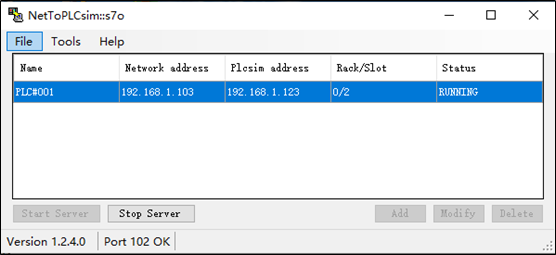
8、添加Station：回到NetToPLCsim软件中，点击Add，添加Station，如下图所示：

9、Start Server：在NetToPLCsim软件中，点击Start Server，如下图所示：

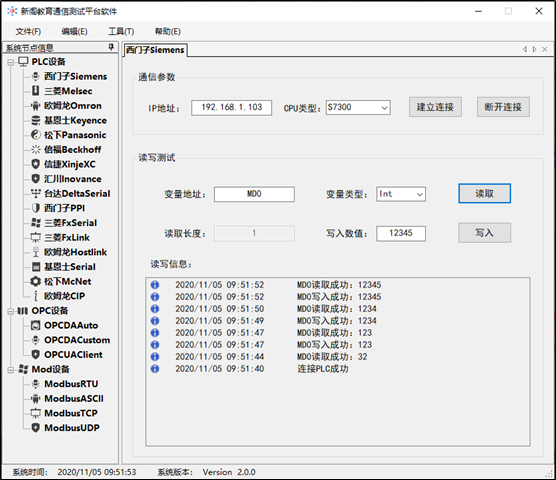
10、通信测试：按照以上步骤执行完成后，一个S7-300PLC的仿真环境就搭建好了，接下来可以进行通信，这里使用的是通信测试平台，设置IP地址为192.168.1.103，PLC类型选择300PLC，读取变量选择MD0（由于没有写任何程序，也没有创建DB块，所以就直接测试M存储区变量），类型选择INT类型，读取并写入数据，进行测试，结果如下所示：【dotNet工控上位机：thinger_swj】

特别注意：这里的IP地址要填写PC的IP地址，而不是PLC的IP地址。

03、整体总结

STEP7仿真最大的好处在于可以使用SIMATIC Manager软件仿真300/400PLC，而不需要安装庞大的博图软件，而且这里主要采用的是NetToPLCsim的方案，也不需要安装PLCSIM-Advanced。

【晶晶助教微信：xiketang777】

【dotNet工控上位机：thinger_swj】