ECC ~ Edge-Conditioned Filter in CNN on Graphs

ECC的卷积操作和常规的二维图像卷积操作都是一种加权平均操作，不同之处在于ECC可以作用在任何图结构上，并且其权重由节点间的边权所决定.

考虑$G=(V,E)$, 其中$|V|=n$ 边 $E \in V*V$ , 其中$|E|=m$, 具有$l \in {0,....l_{max}}$ 前向神经网络. 假设 边和顶点有相同的label, 存在一个

顶点的特征表示为$X^{l}:V \rightarrow \mathbb{R}^{d_{l}}$,  每个边的特征表示 $L: E \rightarrow \mathbb{R}^{s}$,  可以得到顶底的特征矩阵 和 边的特征矩阵:

$X^{l} \in \mathbb{R}^{n * d_{l}}, L \in \mathbb{R}^{m * s}$

顶点i的邻居节点表示为:

$N(i) = {j;(j,i) \in E } \bigcup {i}$

计算顶点$i$ 第l层的特征向量 $X^{l}(i) \in \mathbb{R}^{d_{l}}$, 可以通过l-1层他的邻居节点特征的加权和得到$X^{l-1}(j) \in R^{d_{l}-1}$ , 借用动态滤波器网络的思想,

定义了一个filter-generating 网络(核心):

$F^{l} : R^{s} \rightarrow \mathbb{R}^{d_{l}*d_{l-1}}$

将边标签$L(j,i)$ 作为输入, 输出 每条边决定的权重矩阵:

$\Theta_{j,i}^{l} \in  \mathbb{R}^{d_{l} * d_{l-1}}$

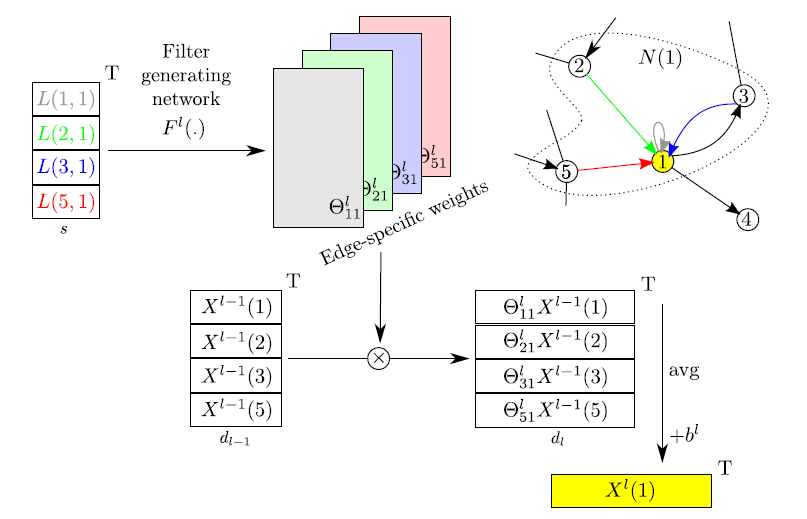
这个边条件卷积(ECC)能够表示为:

$X^{l}(i) =\frac{1}{|N(i)|} \sum_{j \in N(i)} F^{l}(L(j,i),; w^{l}) X^{l-1} (j) + b^{l}$

$= \frac{1}{|N(i)|} \sum_{j \in N(i)} \Theta_{ji}^{l}(j) + b^{l} $

$F^{l}$是由可学习网络权值$w^{l}$的参数化。$\Theta_{ji}^{l}(j)$是为特定输入图中的边标签动态生成的参数。

其中filter-generating 网络$F^{l}$ 能够通过MLP 产生.