利用分块传输绕WAF

分块传输原理介绍

背景

HTTP Connection有两种连接方式：短连接和长连接；

短连接即一次请求对应一次TCP连接的建立和销毁过程。

长连接是多个请求共用同一个连接这样可以节省大量连接建立时间提高通信效率。目前主流浏览器都会在请求头里面包含Connection:keep-alive字段，该字段的作用就是告诉HTTP服务器响应结束后不要关闭连接，浏览器会将建立的连接缓存起来，当在有限时效内有再次对相同服务器发送请求时则直接从缓存中取出连接进行通信。当然被缓存的连接如果空闲时间超过了设定值（如firefox为115s，IE为60s）则会关闭连接。

长连接存在的问题

长连接也叫持续连接，短连接也叫非持续连接。

持续连接存在的问题：对于非持续连接，浏览器可以通过连接是否关闭来界定请求或响应实体的边界；而对于持续连接，这种方法显然不奏效。有时，尽管我已经发送完所有数据，但浏览器并不知道这一点，它无法得知这个打开的连接上是否还会有新数据进来，只能傻傻地等了。

用Content-length解决：计算实体长度，并通过头部告诉对方。浏览器可以通过 Content-Length 的长度信息，判断出响应实体已结束

Content-length引入的新问题：由于 Content-Length 字段必须真实反映实体长度，但是对于动态生成的内容来说，在内容创建完之前，长度是不可知的。这时候要想准确获取长度，只能开一个足够大的buffer，等内容全部生成好再计算。但这样做一方面需要更大的内存开销，另一方面也会让客户端等更久。

我们需要一个新的机制：不依赖头部的长度信息，也能知道实体的边界——分块编码（Transfer-Encoding: chunked）

分块编码（Transfer-Encoding: chunked）

Transfer-Encoding，是一个HTTP头部字段（响应头域），字面意思是「传输编码」，最新的HTTP规范里，只定义了一种编码传输：分块编码(chunked)。

分块传输编码（Chunked transfer encoding）是超文本传输协议（HTTP）中的一种数据传输机制，允许HTTP由网页服务器发送给客户端的数据可以分成多个部分。分块传输编码只在HTTP协议1.1版本（HTTP/1.1）中提供。数据分解成一系列数据块，并以一个或多个块发送，这样服务器可以发送数据而不需要预先知道发送内容的总大小。

分块编码具体方法

在头部加入Transfer-Encoding:chunked之后，就代表这个报文采用了分块编码。这时，报文中的实体需要改为用一系列分块来传输。

每个分块包含十六进制的长度值和数据，长度值独占一行，长度不包括它结尾的CRLF(\r\n)，也不包括分块数据结尾的CRLF。

最后一个分块长度值必须为0，对应的分块数据没有内容，表示实体结束。

消息体格式如下：

hex的分块长度+<CR>回车+<LF>换行
chunked data
结束块的分块长度为0

例如：

如要发送的内容(消息体)为：123456789
那么消息体的格式为：
9<CR><LF>
123456789<CR><LF>
0<CR><LF>

Content-Encoding 和 Transfer-Encoding 二者经常会结合来用，其实就是针对 Transfer-Encoding 的分块再进行 Content-Encoding压缩。

分块传输可以在长度标识处加上分号“;”作为注释，几乎所有可以识别Transfer-Encoding数据包的WAF，都没有处理分块数据包中长度标识处的注释，导致在分块数据包中加入注释的话，WAF就识别不出这个数据包了。如：

9;kkkkk
1234567=1
4;ooo=222
2345
0
(两个换行)

chunked-coding-converter

插件介绍

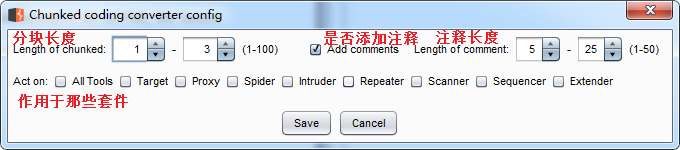
插件下载

github-chunked-coding-converter

分块传输绕安全