PTA甲级—数学

1.简单数学

1008 Elevator (20分)

模拟题

#include <cstdio>
#include <cstring>
#include <string>
#include <algorithm>
#include <iostream>
#include <map>
#include <cmath>
#define ll long long
#define inf 0x3f3f3f
using namespace std;
const int maxn = 1e4+100;
int n, sum, now, tmp;
int main(){
    scanf("%d", &n);
    for(int i = 1; i <= n; i++){
        scanf("%d", &tmp);
        int num = tmp-now;
        sum += num > 0 ? num*6 : num*(-4);
        now = tmp;
    }
    sum += 5*n;
    printf("%d", sum);
}

1049 Counting Ones (30 分)

1的个数等于各个位出现1的次数的累加和，因此我们计算各个位上对答案的贡献即可。

那么关键的问题就在如何计算某一位上的贡献，当然就是求这一位为1时数的个数，如下：

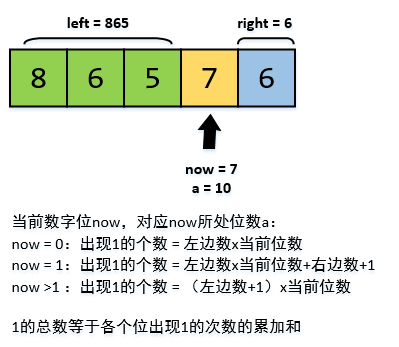（具体为什么是这样可以在脑子或者纸上演算一下）

我一开始的思路是对的，但是那会想不出来具体的做法，考试时暴力骗个分还是可以的。另外上机指南中提到可以对程序进行边界测试，确实应当如此，以后多使用几种方法来测试自己的代码

#include <cstdio>
#include <cstring>
#include <string>
#include <algorithm>
#include <iostream>
#include <vector>
#include <set>
#include <map>
#include <queue>
#define ll long long
#define inf 0x3f3f3f3f
#define pb push_back
#define pii pair<int,int>
using namespace std;
const int maxn = 2e6+100;
int n, res;
int main(){
    scanf("%d", &n);
    int left = n, right, a = 1, now;
    while(left){
        now = left%10, right = n-left*a, left /= 10;
        if(now==0) res += left*a;
        else if(now==1) res += left*a+right+1;
        else res += (left+1)*a;
        a *= 10;
    }
    printf("%d", res);
} 

Reference:

https://blog.csdn.net/CV_Jason/article/details/85112495

1069 The Black Hole of Numbers (20 分)

按照题目要求模拟即可，不过要注意要考虑全面：

1.所有输出都要求4位数

2.考虑特殊样例如6174、2222、1情况下的处理。如输入为1的时候要补充前导0；输入为6174的时候要输出一行而不能直接退出

#include <cstdio>
#include <cstring>
#include <string>
#include <algorithm>
#include <iostream>
#include <vector>
#include <set>
#include <map>
#include <queue>
#define ll long long
#define inf 0x3f3f3f3f
#define pb push_back
#define pii pair<int,int>
using namespace std;
const int maxn = 1e5+100;
string a, b, c, last, s;
int tmp;
int main(){
    cin >> c;
    while(1){
        for(int i = 0; i < 4-c.length(); i++) s += "0";
        s += c, a = b = s, last = c;
        sort(a.begin(), a.end()), sort(b.rbegin(), b.rend());
        c = to_string(stoi(b) - stoi(a)), s.clear();
        printf("%04d - %04d = %04d\n", stoi(b), stoi(a), stoi(c));
        if(c=="6174"||c=="0") break;
    }
}