CF1182E Product Oriented Recurrence

思路：

f_n = c^a_n * f₁^x_n * f₂^y_n * f₃^z_n, 首先dp计算指数部分a_n = a_n-1 + a_n-2 + a_n-3 + 2 * n - 6, 而a_n-1 = a_n-2 + a_n-3 + a_n-4 + 2 * n - 8，相减可以得到a_n = 2 * a_n-1 - a_n-4 + 2。x_n，y_n和z_n是普通的三阶斐波那契。计算完指数部分要对p - 1取模(由费马小定理知p为质数的情况a^{p - 1} % p = 1)，然后再用快速幂计算各个部分相乘即可。

再记录一种两个互相交互的递推式的矩阵快速幂构造：

                    

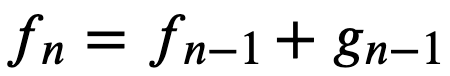
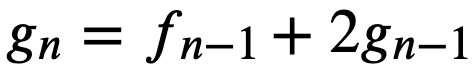
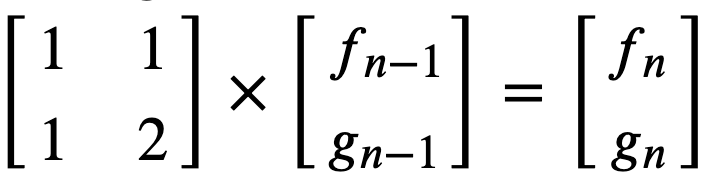
实现：

 #include <bits/stdc++.h>
 using namespace std;

 typedef long long ll;
 typedef vector<vector<ll>> matrix;

 const ll mod = 1e9 + , p_mod = mod - ;

 matrix mat_mul(matrix & a, matrix & b)
 {
     matrix c(a.size(), vector<ll>(b[].size()));
     for (int i = ; i < a.size(); i++)
     {
         for (int k = ; k < a[].size(); k++)
         {
             for (int j = ; j < b[].size(); j++)
             {
                 c[i][j] = ((c[i][j] + a[i][k] * b[k][j] % p_mod) + p_mod) % p_mod;
             }
         }
     }
     return c;
 }

 matrix mat_pow(matrix & a, ll n)
 {
     matrix res(a.size(), vector<ll>(a[].size()));
     for (int i = ; i < a.size(); i++) res[i][i] = ;
     while (n > )
     {
         if (n & ) res = mat_mul(res, a);
         a = mat_mul(a, a);
         n >>= ;
     }
     return res;
 }

 ll pow(ll x, ll n)
 {
     ll res = ;
     while (n > )
     {
         if (n & ) res = res * x % mod;
         x = x * x % mod;
         n >>= ;
     }
     return res;
 }

 int main()
 {
     ll n, f1, f2, f3, c;
     while (cin >> n >> f1 >> f2 >> f3 >> c)
     {
         matrix x(, vector<ll>(, )), a(, vector<ll>(, ));
         x[][] = ; x[][] = -; x[][] = ;
         x[][] = x[][] = x[][] = x[][] = ;
         a[][] = ; a[][] = ;
         matrix c_p = mat_pow(x, n - );
         c_p = mat_mul(c_p, a);
         matrix y(, vector<ll>(, )), b1(, vector<ll>(, )), b2(, vector<ll>(, )), b3(, vector<ll>(, ));
         y[][] = y[][] = y[][] = y[][] = y[][] = ;
         b1[][] = b2[][] = b3[][] = ;
         matrix t = mat_pow(y, n - );
         matrix f1_p = mat_mul(t, b1);
         matrix f2_p = mat_mul(t, b2);
         matrix f3_p = mat_mul(t, b3);
         ll ans = ;
         ans = ans * pow(c, c_p[][]) % mod;
         ans = ans * pow(f1, f1_p[][]) % mod;
         ans = ans * pow(f2, f2_p[][]) % mod;
         ans = ans * pow(f3, f3_p[][]) % mod;
         cout << ans << endl;
     }
     return ;
 }