洛谷P3384【模板】树链剖分

题目描述

如题，已知一棵包含\(N\)个结点的树（连通且无环），每个节点上包含一个数值，需要支持以下操作：

操作\(1\)： 格式： \(1\) \(x\) \(y\) \(z\) 表示将树从\(x\)到\(y\)结点最短路径上所有节点的值都加上\(z\)

操作\(2\)： 格式： \(2\) \(x\) \(y\) 表示求树从\(x\)到\(y\)结点最短路径上所有节点的值之和

操作\(3\)： 格式： \(3\) \(x\) \(z\) 表示将以\(x\)为根节点的子树内所有节点值都加上\(z\)

操作\(4\)： 格式： \(4\) \(x\) 表示求以\(x\)为根节点的子树内所有节点值之和

输入输出格式

输入格式：

第一行包含\(4\)个正整数\(N\)、\(M\)、\(R\)、\(P\)，分别表示树的结点个数、操作个数、根节点序号和取模数（即所有的输出结果均对此取模）。

接下来一行包含\(N\)个非负整数，分别依次表示各个节点上初始的数值。

接下来\(N-1\)行每行包含两个整数\(x\)、\(y\)，表示点\(x\)和点\(y\)之间连有一条边（保证无环且连通）

接下来\(M\)行每行包含若干个正整数，每行表示一个操作，格式如下：

操作\(1\)： \(1\) \(x\) \(y\) \(z\)

操作\(2\)： \(2\) \(x\) \(y\)

操作\(3\)： \(3\) \(x\) \(z\)

操作\(4\)： \(4\) \(x\)

输出格式：

输出包含若干行，分别依次表示每个操作\(2\)或操作\(4\)所得的结果（对\(P\)取模）

输入输出样例

输入样例#1：

5 5 2 24
7 3 7 8 0
1 2
1 5
3 1
4 1
3 4 2
3 2 2
4 5
1 5 1 3
2 1 3

输出样例#1：

2
21

说明

时空限制：\(1s\)，\(128M\)

数据规模：

对于\(30\%\)的数据： \(N \leq 10, M \leq 10\)

对于\(70\%\)的数据： \(N \leq {10}^3, M \leq {10}^3\)

对于\(100\%\)的数据： \(N \leq {10}^5, M \leq {10}^5\)

（ 其实，纯随机生成的树\(LCA\)+暴力是能过的，可是，你觉得可能是纯随机的么\(233\)）

样例说明：

树的结构如下：

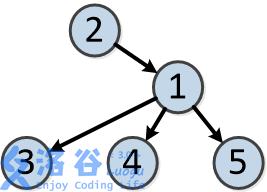
各个操作如下：

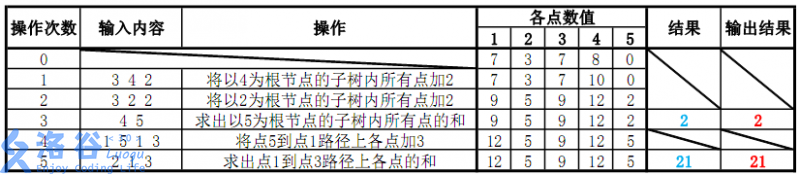
故输出应依次为\(2\)、\(21\)(重要的事情说三遍：记得取模)

思路：思路在课件里面写过了，不想再写一遍了……就是一个树链剖分加线段树的板子题。

代码：

#include<cstdio>
#include<algorithm>
#include<cctype>
#define maxn 100007
#define ll long long
#define ls rt<<1
#define rs rt<<1|1
using namespace std;
int mod,head[maxn],d[maxn],sum[maxn<<2],a[maxn];
int num,cnt,n,m,lazy[maxn<<2],fa[maxn],id[maxn];
int rt,w[maxn],top[maxn],size[maxn],son[maxn];
inline int qread() {
    char c=getchar();int num=0,f=1;
    for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
    for(;isdigit(c);c=getchar()) num=num*10+c-'0';
    return num*f;
}
struct node {
    int v,nxt;
}e[maxn<<1];
inline void ct(int u, int v) {
    e[++num].v=v;
    e[num].nxt=head[u];
    head[u]=num;
}
inline void pushup(int rt) {
    sum[rt]=(sum[ls]+sum[rs])%mod;
}
void build(int rt, int l, int r) {
    if(l==r) {
        sum[rt]=a[l];
        return;
    }
    int mid=(l+r)>>1;
    build(ls,l,mid);
    build(rs,mid+1,r);
    pushup(rt);
}
inline void pushdown(int rt, int len) {
    if(lazy[rt]) {
        lazy[ls]+=lazy[rt],lazy[ls]%=mod;
        lazy[rs]+=lazy[rt],lazy[rs]%=mod;
        sum[ls]+=(len-(len>>1))*lazy[rt],sum[ls]%=mod;
        sum[rs]+=(len>>1)*lazy[rt],sum[rs]%=mod;
        lazy[rt]=0;
    }
}
void modify(int rt, int l, int r, int L, int R, int val) {
    if(L>r||R<l) return;
    if(L<=l&&r<=R) {
        sum[rt]+=val*(r-l+1),sum[rt]%=mod;
        lazy[rt]+=val,lazy[rt]%=mod;
        return;
    }
    int mid=(l+r)>>1;
    pushdown(rt,r-l+1);
    modify(ls,l,mid,L,R,val),modify(rs,mid+1,r,L,R,val);
    pushup(rt);
}
int csum(int rt, int l, int r, int L, int R) {
    if(L>r||R<l) return 0;
    if(L<=l&&r<=R) return sum[rt];
    int mid=(l+r)>>1;
    pushdown(rt,r-l+1);
    return csum(ls,l,mid,L,R)+csum(rs,mid+1,r,L,R);
}
void dfs1(int u, int f) {
    size[u]=1;
    for(int i=head[u];i;i=e[i].nxt) {
        int v=e[i].v;
        if(v!=f) {
        	d[v]=d[u]+1;
        	fa[v]=u;
        	dfs1(v,u);
            size[u]+=size[v];
        	if(size[v]>size[son[u]]) son[u]=v;
        }
    }
}
void dfs2(int u, int t) {
    id[u]=++cnt;
    a[cnt]=w[u];
    top[u]=t;
    if(son[u]) dfs2(son[u],t);
    for(int i=head[u];i;i=e[i].nxt) {
        int v=e[i].v;
        if(v!=fa[u]&&v!=son[u]) dfs2(v,v);
    }
}
int calc(int x, int y) {
    int ans=0;
    int fx=top[x],fy=top[y];
    while(fx!=fy) {
        if(d[fx]<d[fy]) swap(x,y),swap(fx,fy);
        ans+=csum(1,1,cnt,id[fx],id[x]);
        x=fa[fx],fx=top[x];
    }
    if(id[x]>id[y]) swap(x,y);
    ans+=csum(1,1,cnt,id[x],id[y]);
    return ans;
}
void cal(int x, int y, int val) {
    int fx=top[x],fy=top[y];
    while(fx!=fy) {
        if(d[fx]<d[fy]) swap(x,y),swap(fx,fy);
        modify(1,1,cnt,id[fx],id[x],val);
        x=fa[fx],fx=top[x];
    }
    if(id[x]>id[y]) swap(x,y);
    modify(1,1,cnt,id[x],id[y],val);
}
int main() {
    n=qread(),m=qread(),rt=qread(),mod=qread();
    for(int i=1;i<=n;++i) w[i]=qread(),w[i]%=mod;
    for(int i=1,u,v;i<n;++i) {
        u=qread(),v=qread();
        ct(u,v);ct(v,u);
    }
    d[rt]=1,fa[rt]=1;
    dfs1(rt,0);dfs2(rt,rt);build(1,1,n);
    for(int i=1,k,x,y,z;i<=m;++i) {
        k=qread();
        if(k==1) {
            x=qread(),y=qread(),z=qread();
            cal(x,y,z%mod);
        }
        if(k==2) {
            x=qread(),y=qread();
            printf("%d\n",calc(x,y)%mod);
        }
        if(k==3) {
            x=qread(),y=qread();
            modify(1,1,n,id[x],id[x]+size[x]-1,y%mod);
        }
        if(k==4) {
            x=qread();
            printf("%d\n",csum(1,1,n,id[x],id[x]+size[x]-1)%mod);
        }
    }
    return 0;
}